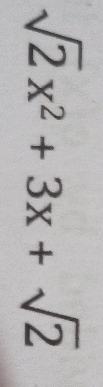CBSE Class 9 Answered
Question is
Asked by 100.akash | 16 Sep, 2008, 04:13: PM
.jpg)
let BP = CQ =b and side of square be a.
we have to prove AQ is perpendicular to DP.
in vector form AQ = AB + BQ
and DP = DA + AP
taking dot product of AQ and DP
=AB.DA + AB.AP +BQ.DA + BQ.AP
now AB & DA and BQ &AP are perpendicular to each other so there dot product will be zero.
=AB.AP + BQ.DA ( |AB|=|DA| = a , |BQ|=|AP| = a+b)
=a(a+b) - (a+b)a ( BQ and DA are in opposite direction so a negative sign comes)
=0
since AQ.DP = 0 i.e. AQ and DP are perpendicular to each other.
Answered by | 18 Dec, 2008, 08:22: PM
Application Videos
Concept Videos
CBSE 9 - Maths
Asked by rathorgaurav2945 | 21 Apr, 2024, 10:31: PM
CBSE 9 - Maths
Asked by monika.vns14 | 18 Apr, 2024, 05:15: PM
CBSE 9 - Maths
Asked by gulshanelectronics2017 | 15 Apr, 2024, 05:35: PM
CBSE 9 - Maths
Asked by tripura78839 | 12 Apr, 2024, 09:05: PM
CBSE 9 - Maths
Asked by singhanjali0199 | 12 Apr, 2024, 08:29: PM
CBSE 9 - Maths
Asked by killerstealer593 | 11 Apr, 2024, 07:50: PM
CBSE 9 - Maths
Asked by saee.shinde3069 | 31 Mar, 2024, 10:12: PM
CBSE 9 - Maths
Asked by rathoreraj7296 | 31 Mar, 2024, 08:09: PM
CBSE 9 - Maths
Asked by divyanshibirla037 | 29 Mar, 2024, 03:26: PM