CBSE Class 11-science Answered
Q. Calculate the sum of the squares of first 100 terms of an AP , given that the sum of the first 100 terms is -1. and that the sum of 2nd , 4th, ......., 100th term is 1.
Asked by Shrivatsa | 22 Nov, 2018, 17:36: PM
In A.P, sum of 100 terms is -1, (100/2) [ 2a +99d ] = 50 [ 2a+99d ] = -1 .................(1)
where a is the first term and d is common difference. eqn.(1) can be rewritten as [ 2a + 99d ] = (-1/50) ...................(2)
Similarly if sum of 2nd, 4th, 6th .......100th terms are -1 , then (50/2) [ 2(a+d) + 49×2d ] = 1 or 2a+100d = (1/25) ...............(3)
if we solve eqns. (2) and (3), we get d = 3/50 and a = -149/50
we can write the nth term of A.P. as, tn = (-149/50)+(n-1)(3/50)
Hence the required sum = 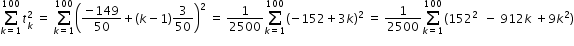 .....................(4)
.....................(4)
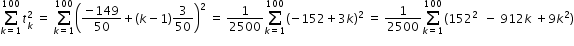 .....................(4)
.....................(4)In eqn.(4) we get sum of integers and sum of squares of integers from 1 to 100.
Hence the required sum as given in eqn.(4) is written as 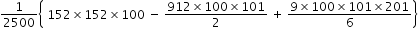
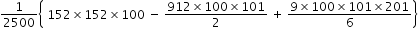
further simplification can done by the student
Answered by Thiyagarajan K | 23 Nov, 2018, 22:02: PM
Application Videos
Concept Videos
CBSE 11-science - Maths
Asked by megaladevi07 | 24 Jul, 2024, 11:01: AM
CBSE 11-science - Maths
Asked by mihirkumarjha356 | 18 Jul, 2024, 21:51: PM
CBSE 11-science - Maths
Asked by vijaya198724 | 08 Jul, 2024, 22:33: PM
CBSE 11-science - Maths
Asked by shshnkmanjula | 08 Jul, 2024, 17:25: PM
CBSE 11-science - Maths
Asked by harshdasisode | 04 Jul, 2024, 00:07: AM
CBSE 11-science - Maths
Asked by manjushakothavade1979 | 25 Jun, 2024, 10:29: AM
CBSE 11-science - Maths
Asked by ishanvi.pahil | 22 Jun, 2024, 22:31: PM
CBSE 11-science - Maths
Asked by jagathaiah.kamsali | 13 Jun, 2024, 20:20: PM
CBSE 11-science - Maths
Asked by nandhandheeraj7474 | 11 Jun, 2024, 17:23: PM
CBSE 11-science - Maths
Asked by nvprithica | 07 Jun, 2024, 11:53: AM












