CBSE Class 11-science Answered
Prove the following by using the principle of mathematical induction for all n ? N: 1.3+3.5+5.7+...+(2n-1)(2n+1)=(n(4n^2+6n-1))/3
Asked by shweta tyagi | 25 Jul, 2012, 06:43: PM
For n = 1.
LHS = (2(1) - 1)(2(1) + 1) = 1(3) = 3.
RHS = [1(4(1^2) + 6(1) - 1)]/3 = [(4 + 6 - 1)]/3 = 9/3 = 3.
Therefore the statement holds for n = 1.
LHS = (2(1) - 1)(2(1) + 1) = 1(3) = 3.
RHS = [1(4(1^2) + 6(1) - 1)]/3 = [(4 + 6 - 1)]/3 = 9/3 = 3.
Therefore the statement holds for n = 1.
Assume the statement is true for n = k and prove that it is true for n = (k + 1).
The statement for n = k can be written as
1.3+3.5+5.7+.....+(2k-1)(2k+1) = [k(4k² + 6k -1)]/3
Adding (2(k+1) - 1)(2(k+1) + 1) to both sides, we have
1.3+3.5+5.7+.....+(2k-1)(2k+1) + (2(k+1) - 1)(2(k+1) + 1) = [k(4k² + 6k -1)]/3 + (2(k+1) - 1)(2(k+1) + 1)
= [k(4k² + 6k -1)]/3 + (2k+1)(2k+3)
= [k(4k² + 6k -1)]/3 + (4k^2 + 8k +3)
= [k(4k² + 6k -1)]/3 + 3(4k^2 + 8k +3)/3
= [k(4k² + 6k -1)]/3 + (12k^2 + 24k +9)/3
= [k(4k² + 6k -1) + 12k^2 + 24k +9]/3
= [4k^3 + 6k^2 - k + 12k^2 + 24k +9]/3
= [4k^3 + 18k^2 + 23k +9]/3
= [(k+1)(4k^2 + 14k + 9)]/3
= [(k+1)(4k^2 + 8k + 4 + 6k + 6 - 1)]/3
= [(k+1)(4(k^2 + 2k + 1) + 6(k+1) - 1)]/3
= [(k+1)(4(k+1)^2 + 6(k+1) - 1)]/3
Therefore we have
1.3+3.5+5.7+.....+(2k-1)(2k+1) + (2(k+1) - 1)(2(k+1) + 1) = [(k+1)(4(k+1)^2 + 6(k+1) - 1)]/3,
Thus, the statement for n = (k+1) assuming it is true for n = k.
Hence, by the Principle of Mathematical Induction, the statement
1.3+3.5+5.7+.....+(2n-1)(2n+1) = [n(4n² + 6n -1)]/3
is true for all positive integers n.
The statement for n = k can be written as
1.3+3.5+5.7+.....+(2k-1)(2k+1) = [k(4k² + 6k -1)]/3
Adding (2(k+1) - 1)(2(k+1) + 1) to both sides, we have
1.3+3.5+5.7+.....+(2k-1)(2k+1) + (2(k+1) - 1)(2(k+1) + 1) = [k(4k² + 6k -1)]/3 + (2(k+1) - 1)(2(k+1) + 1)
= [k(4k² + 6k -1)]/3 + (2k+1)(2k+3)
= [k(4k² + 6k -1)]/3 + (4k^2 + 8k +3)
= [k(4k² + 6k -1)]/3 + 3(4k^2 + 8k +3)/3
= [k(4k² + 6k -1)]/3 + (12k^2 + 24k +9)/3
= [k(4k² + 6k -1) + 12k^2 + 24k +9]/3
= [4k^3 + 6k^2 - k + 12k^2 + 24k +9]/3
= [4k^3 + 18k^2 + 23k +9]/3
= [(k+1)(4k^2 + 14k + 9)]/3
= [(k+1)(4k^2 + 8k + 4 + 6k + 6 - 1)]/3
= [(k+1)(4(k^2 + 2k + 1) + 6(k+1) - 1)]/3
= [(k+1)(4(k+1)^2 + 6(k+1) - 1)]/3
Therefore we have
1.3+3.5+5.7+.....+(2k-1)(2k+1) + (2(k+1) - 1)(2(k+1) + 1) = [(k+1)(4(k+1)^2 + 6(k+1) - 1)]/3,
Thus, the statement for n = (k+1) assuming it is true for n = k.
Hence, by the Principle of Mathematical Induction, the statement
1.3+3.5+5.7+.....+(2n-1)(2n+1) = [n(4n² + 6n -1)]/3
is true for all positive integers n.
Answered by | 25 Jul, 2012, 10:14: PM
Concept Videos
CBSE 11-science - Maths
Asked by keeruzzzzz | 11 Mar, 2020, 07:35: PM
CBSE 11-science - Maths
Asked by syedaliasad649 | 01 Oct, 2019, 07:07: PM
CBSE 11-science - Maths
Asked by lovemaan5500 | 02 Feb, 2019, 08:24: PM
CBSE 11-science - Maths
Asked by Topperlearning User | 14 May, 2014, 03:21: PM
CBSE 11-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 11-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 11-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 11-science - Maths
Asked by Topperlearning User | 07 Aug, 2014, 08:49: AM
CBSE 11-science - Maths
Asked by Topperlearning User | 15 May, 2014, 10:48: AM
CBSE 11-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM







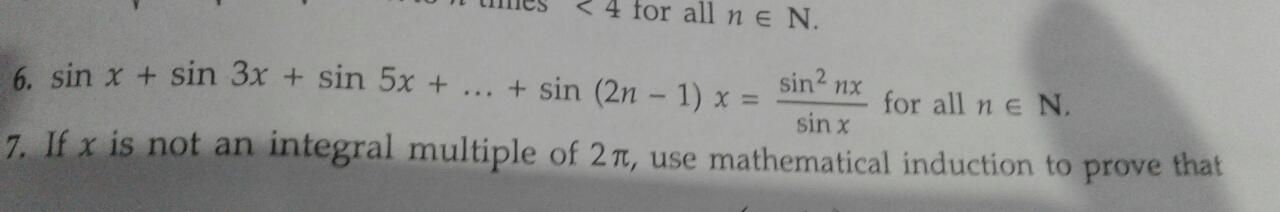
 n(3n-1)
n(3n-1)