CBSE Class 11-science Answered
Explain the principle of mathematical induction:
Asked by Topperlearning User | 15 May, 2014, 10:48: AM
Suppose there is a given statement P(n) involving the natural number 'n' such that
(i) The statement is true for n = 1, i. e. P(1) is true, and
(ii) If the statement is true for n = k (where k is some positive integer), then the statement is also true for n = k + 1, i.e. truth of P(k) implies the truth of P(k +1).
Then, P(n) is true for all natural numbers n.
Answered by | 15 May, 2014, 12:48: PM
Concept Videos
CBSE 11-science - Maths
Asked by keeruzzzzz | 11 Mar, 2020, 07:35: PM
CBSE 11-science - Maths
Asked by Topperlearning User | 14 May, 2014, 03:21: PM
CBSE 11-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 11-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 11-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 11-science - Maths
Asked by Topperlearning User | 07 Aug, 2014, 08:49: AM
CBSE 11-science - Maths
Asked by Topperlearning User | 15 May, 2014, 10:48: AM
CBSE 11-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 11-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 11-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM





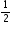 n(3n-1)
n(3n-1)