CBSE Class 11-science Answered
Prove that x^(2n-1)+y^(2n-1) is divisible by x+y for all n belongs to N.
Asked by Benjamin | 21 Sep, 2015, 05:41: PM

Answered by Vijaykumar Wani | 22 Sep, 2015, 12:02: PM
Concept Videos
CBSE 11-science - Maths
Asked by keeruzzzzz | 11 Mar, 2020, 07:35: PM
CBSE 11-science - Maths
Asked by syedaliasad649 | 01 Oct, 2019, 07:07: PM
CBSE 11-science - Maths
Asked by lovemaan5500 | 02 Feb, 2019, 08:24: PM
CBSE 11-science - Maths
Asked by Topperlearning User | 14 May, 2014, 03:21: PM
CBSE 11-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 11-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 11-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 11-science - Maths
Asked by Topperlearning User | 07 Aug, 2014, 08:49: AM
CBSE 11-science - Maths
Asked by Topperlearning User | 15 May, 2014, 10:48: AM
CBSE 11-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM







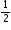 n(3n-1)
n(3n-1)