CBSE Class 10 Answered
Prove that the area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of its diagonals.
Asked by pulakananda | 30 Aug, 2010, 12:00: AM
Answered by | 30 Aug, 2010, 09:47: AM
Application Videos
Concept Videos
CBSE 10 - Maths
Asked by suryapalsinghgoudmahirajbanna | 17 Sep, 2023, 10:50: PM
CBSE 10 - Maths
Asked by bnarayanamstr | 03 May, 2023, 10:03: AM
CBSE 10 - Maths
Asked by savitamahajan202 | 30 Dec, 2022, 12:51: PM
CBSE 10 - Maths
Asked by bhu.joshi54 | 04 Jul, 2022, 08:18: PM
CBSE 10 - Maths
Asked by bhu.joshi54 | 16 Jun, 2022, 07:56: PM
CBSE 10 - Maths
Asked by dishapalnati82 | 24 Nov, 2021, 09:30: AM
CBSE 10 - Maths
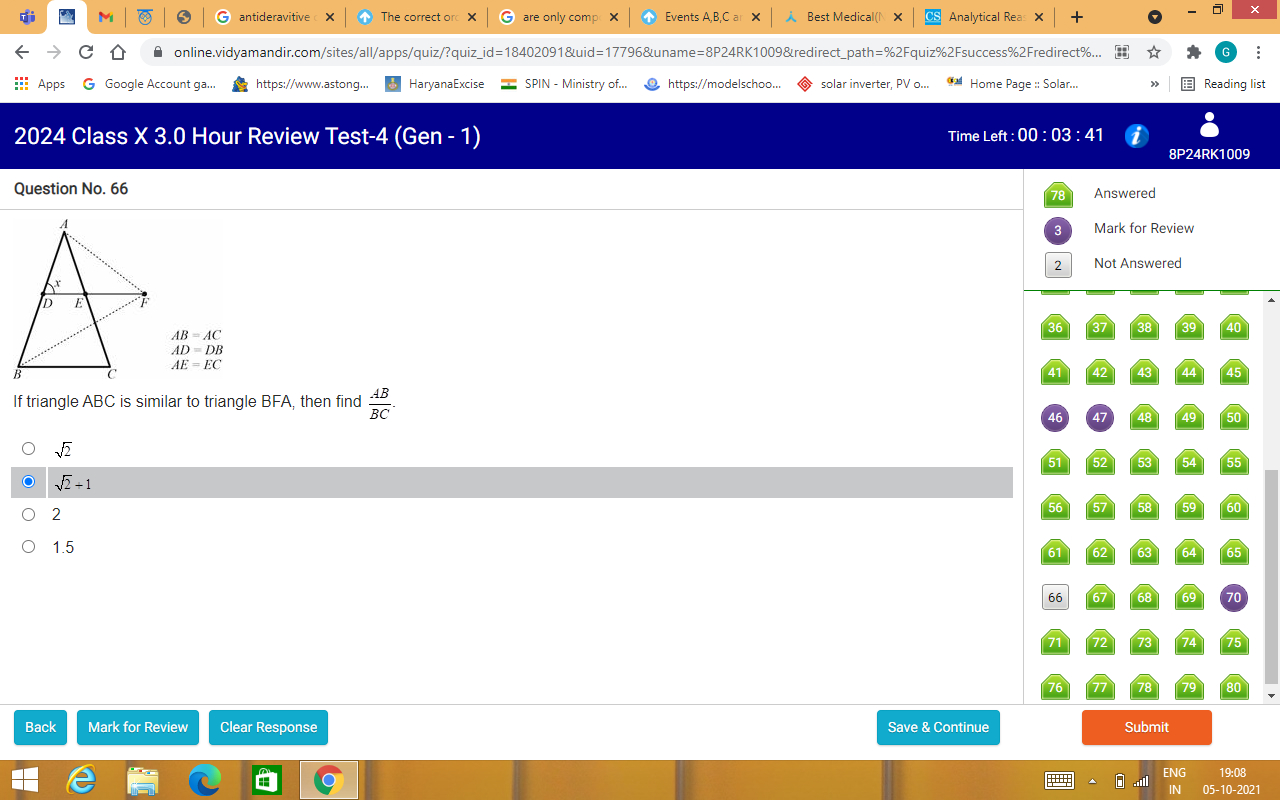
Asked by psinghaladv | 05 Oct, 2021, 07:49: PM