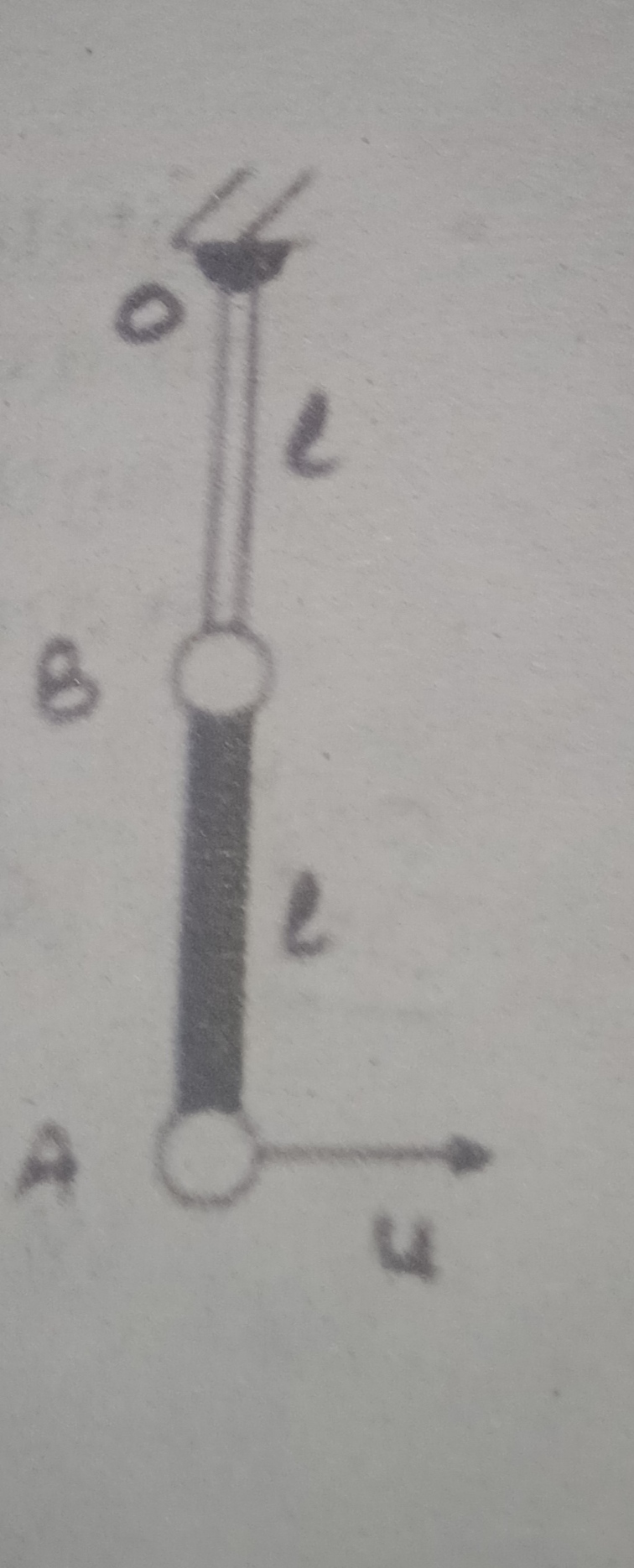Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 12-science Answered

please explain elaborately
question image
Asked by nelsonsanabam46 | 13 Nov, 2020, 06:29: PM
answered-by-expert Expert Answer
By Ampere's law , magnetic field induction B  near current carrying wire is given as
 
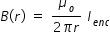begin mathsize 14px style B left parenthesis r right parenthesis space equals space fraction numerator mu subscript o over denominator 2 pi r end fraction space I subscript e n c end subscript end style  .........................(1)
where μo is permeability of free space , r is radial distance from central axis of wire and
Ienc is enclosed current within the circle of radius drawn with axis of wire as centre.
 
Let I be the current passing through wire of circular cross section radius R .
 
At a point , which is at distance r from centre of wire crosssection , within the wire ( r < R ),
magnetic field induction B(r) is obtained from eqn.(1) by substituting enclosed current.
 
Ienc = crosssection area of radius r × current density =  ( π r2 ) × [  I / ( π R2 ) ] = I × ( r2 / R2 )
 
where I is the current passing through wire.
 
Magnetic field induction B(r)  , when r < R is given as
 
begin mathsize 14px style B left parenthesis r right parenthesis space equals space fraction numerator mu subscript o over denominator 2 pi r end fraction cross times I space r squared over R squared space equals space fraction numerator mu subscript o space I over denominator 2 pi end fraction cross times open parentheses r over R squared close parentheses end style...................................(2)
 
 
At a radial distance r = R , i.e., when the point is on the surface of wire ,
Magnetic field induction B(r) is obtained from eqn.(2) by substituting r = R
 
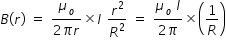begin mathsize 14px style B left parenthesis r right parenthesis space equals space fraction numerator mu subscript o over denominator 2 pi r end fraction cross times I space r squared over R squared space equals space fraction numerator mu subscript o space I over denominator 2 pi end fraction cross times open parentheses 1 over R close parentheses end style ....................... (3)
At a radial distance r > R , i.e., when the point is outside the wire , enclosed current is simply I
 
Hence we get magnetic field induction B from eqn.(1) as
 
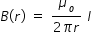
begin mathsize 14px style B left parenthesis r right parenthesis space equals space fraction numerator mu subscript o over denominator 2 pi r end fraction space I end style
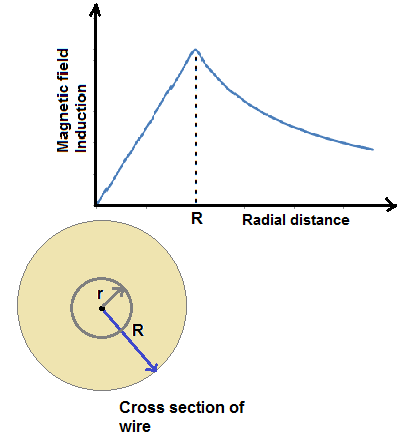
Plot of the magnetic field induction as a finction of radial distance is shown in figure.
Answered by Thiyagarajan K | 14 Nov, 2020, 10:29: AM

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 12-science - Physics
explain this concept
question image
Asked by panneer1766 | 24 Apr, 2024, 01:52: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
A dumbbell consists of two masses A and B each of mass m joined by a light rod of length l with mass B attached to a suspension point O by a light rod of length l as shown in figure. Find the minimum required speed with which mass A to be projected horizontally so that the system completes the vertical circular motion.
question image
Asked by artabandhusahu85 | 24 Apr, 2024, 12:07: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
What is charge?
Asked by niharvijayvargiya5 | 23 Apr, 2024, 06:40: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
please resolve with good explanation
question image
Asked by kulhariabhijeet | 21 Apr, 2024, 02:39: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
what are ghost particles please answer how is that not able to interact with other subatomic particles ..?is that faster than photons?
Asked by mohapatraswetalina88 | 21 Apr, 2024, 12:18: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
if breakdown voltage of each capacitor is 40v ,then maximum applied voltage Vmax will be
Asked by aishaisha091098 | 19 Apr, 2024, 04:54: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
explain
question image
Asked by ranadeb8090 | 19 Apr, 2024, 03:32: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
solve option e
question image
Asked by dasrituparna1999 | 13 Apr, 2024, 06:56: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
The number of moles in an elemental sample is just the ratio of the mass m to atomic mass 4. n= A The number of protons N, in an elemental sample is Z (atomic number) times the number of moles of Avogadro's number NA N=ZnN P A Copper has an atomic mass of 63.5 g/mole and 29 protons per atom. If such an atom were neutral, then it would have as many protons as electrons. If you remove electrons from a neutral state, then you get a net positive charge. Given a 54 gram ball of copper with a net charge of 2.2 µC, what fraction of the copper's electrons have been removed?
Asked by dasrituparna1999 | 12 Apr, 2024, 09:26: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
which answer is correct and most appropriate with explanation
question image
Asked by mishrigupta19319 | 08 Apr, 2024, 06:28: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×