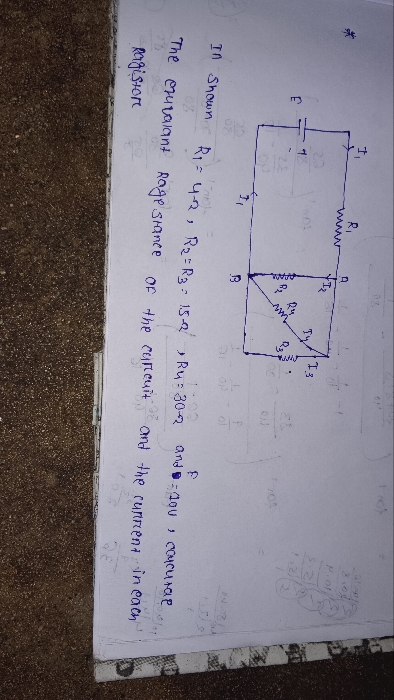
CBSE Class 12-science Answered
Pl ans

Asked by jain.pradeep | 16 Feb, 2020, 08:29: PM
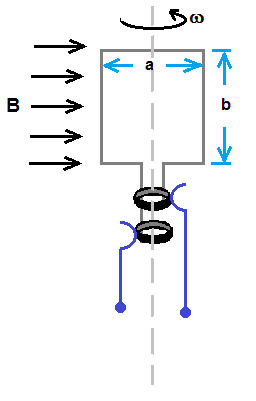
Figure shows a rectangular coil of width a and length b is rotating in a uniform magnetic field.
Induced emf E in the coil is given as, E = -dφ/dt , where φ is magnetic flux
magnetic flux = B•A = B (ab) cosθ where B is magnetic flux density, A is area of coil that equals (a b)
and θ is the angle made by coil with magnetic field direction.
Hence emf E = - (d/dt )[ B (ab) cosθ ] = - (d/dt )[ B (ab) cos(ωt) ] = B (ab) ω sin(ωt)
current i = ( induced emf ) / ( Resistance of coil ) = { [ B (ab) ω ] / R } sin(ωt)
Peak value of emf = B (ab) ω
Peak value of current = { [ B (ab) ω ] / R }
Graph of emf as a function of t is shown in figure
Answered by Thiyagarajan K | 17 Feb, 2020, 12:24: PM
Concept Videos
CBSE 12-science - Physics
Asked by ankush76728 | 06 May, 2024, 04:52: PM
CBSE 12-science - Physics
Asked by ankush76728 | 05 May, 2024, 09:55: PM
CBSE 12-science - Physics
Asked by heymindurownbusiness | 04 May, 2024, 11:15: AM
CBSE 12-science - Physics
Asked by talulu | 01 May, 2024, 05:14: PM
CBSE 12-science - Physics
Asked by kanishkg511 | 30 Apr, 2024, 07:25: PM
CBSE 12-science - Physics
Asked by sahoobanita89 | 30 Apr, 2024, 05:10: AM
CBSE 12-science - Physics
Asked by divakar.9124 | 27 Apr, 2024, 10:42: PM
CBSE 12-science - Physics
Asked by panneer1766 | 24 Apr, 2024, 01:52: PM