CBSE Class 12-science Answered
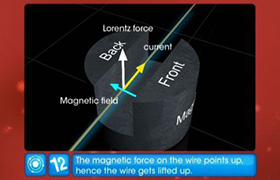
Let us consider an infinitesimal segment of the loop of length ds.
The magnetic field is perpendicular to all the segments of the loop.
Force on this segment, dF = iBds
Horizontal component of the force, dFH = (iB cosθ)ds
This component of the force points away from the loop.
Vertical component of the force, dFv = (iB sinθ)ds
This component of the force points upward from the plane of the loop.
When we sum each of these components for all segments of the loop, the sum of horizontal component of the force vanishes. This happens because the horizontal force acting on the diametrically -opposite segments of the loop cancel each other out. As a result, only the vertical component of the force contributes to the net force on the loop.
The vertical component, which points upward, is
Fv = iB 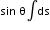 = (2
= (2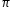 a)iB sinθ (Since i,B, θ are constants)
a)iB sinθ (Since i,B, θ are constants)