CBSE Class 12-science Answered
A circular coil of 200 turns and radius 10 cm is placed in a uniform magnetic field of 0.5 T, normal to the plane of the coil. If the current in the coil is 3.0 A, calculate the
(a) Total torque on the coil
(b) Total force on the coil
(c) Average force on each electron in the coil due to the magnetic field
Assume the area of cross-section of the wire to be 10-5m2 and the free electron density is 1029/m3.
Asked by Topperlearning User | 28 Apr, 2015, 13:54: PM
Here n = 200, r = 10 cm = 0.1 m
B = 0.5 T, I = 3 A
(a) Torque is given by the relation:
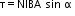
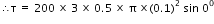
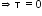
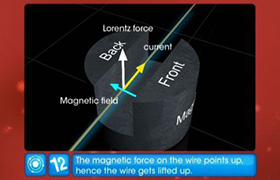
(b) The total force on a current loop placed in a magnetic field is always zero.
(c) Given N = 1029/m3, A = 10-5m2
Average force on an electron of charge (e), moving with drift velocity (Vd) in the magnetic field (B), is given by:
F = BeVd

Answered by | 28 Apr, 2015, 15:54: PM
Concept Videos
CBSE 12-science - Physics
Asked by Topperlearning User | 20 May, 2015, 14:09: PM
CBSE 12-science - Physics
Asked by Topperlearning User | 28 Apr, 2015, 14:05: PM
CBSE 12-science - Physics
Asked by Topperlearning User | 20 May, 2015, 14:11: PM
CBSE 12-science - Physics
Asked by Topperlearning User | 20 May, 2015, 14:14: PM
CBSE 12-science - Physics
Asked by Topperlearning User | 20 May, 2015, 14:33: PM
CBSE 12-science - Physics
Asked by Topperlearning User | 28 Apr, 2015, 13:54: PM
CBSE 12-science - Physics
Asked by Topperlearning User | 20 May, 2015, 14:36: PM
CBSE 12-science - Physics
Asked by Topperlearning User | 20 May, 2015, 14:50: PM
CBSE 12-science - Physics
Asked by Topperlearning User | 20 May, 2015, 14:56: PM
CBSE 12-science - Physics
Asked by Topperlearning User | 20 May, 2015, 15:06: PM