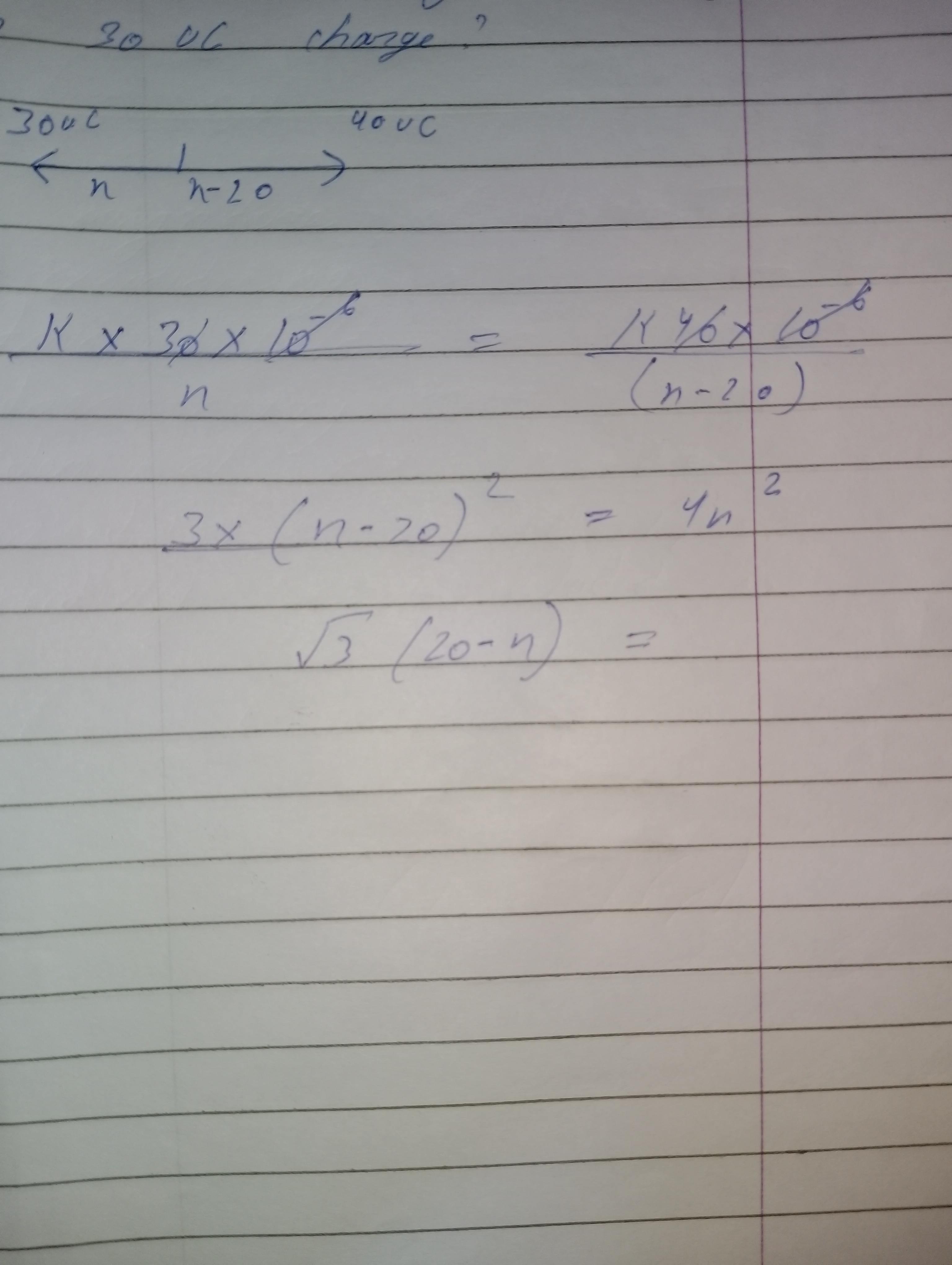CBSE Class 12-science Answered
ln a Millikan’s oil drop experiment, the horizontal plates are 1.5 cm apart. With the electric field switch off an oil drop is observed to fall with a steady velocity of 2.5×10^{-2} cm s^{-1}. When the field is switched on the upper plate being positive, the drop just remains stationary when the p.d. between the plates is 1500 V. Calculate the radius of drop (b) How many electronic charges does it carry? (c)If the p.d. between the two plates remains unchanged, with what velocity will the drop move when it has collected two more as a result of exposure to ionising radiation? (Oil density, rho=900 kgm^{3} , Viscosity of air, eta =1.8×10^{-5} Nsm^{-2}, Density of air, σ=1.293 kg m^{-3})
Asked by arjunsah797 | 01 Apr, 2022, 07:31: AM
Expert Answer
When oil drop moves down with constant terminal velocity , force of gravity Fg on oil is balanced
by buoyancy force Fb and viscous drag Fd on oil .
Fg = Fb + Fd
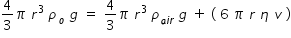
where r is radius of oil drop , ρo is oil density , ρair is density of air , g is acceleration due to gravity ,
η is coefficient of viscosity and v is terminal velocity .
From above expression, we get relation for radius of drop as
----------------------------------
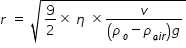
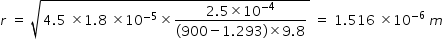
when oil drop remains stationary, Charge on it is obtained by balancing
the force of gravity Fg and electorstaic force Fe
Fg = Fe
m g = q E .......................(1)
where m is mass of oil drop , g is acceleration due to gravity , q is charge on oil drop
and E is electric field intensity
m = (4/3) π r3 ρo g = (4/3) π ( 1.516 × 10-6 )3 × 900 × 9.8 = 1.287 × 10-13 kg
E = V / d = 1500 / 0.015 = 105 V/m
Where V is potential difference between plates and d is separation distance between plates
q = ( 1.287 × 10-13 × 9.8 ) / 105 = 1.261 × 10-17 C
Number of electronic charges = q / e = ( 1.261 × 10-17 ) / ( 1.602 × 10-19 ) ≈ 79
------------------------------------------------
when excess charge of 2 electrons are added to oil drop , oil drop will move upwards due to electrostatic force
and attains terminal velocity v again due to drag force .
Force balance equation is given as
Fe + Fb = Fg + Fd
[ ( q+2) eE ] + [ (4/3) π r3 ρair g ] = [ m g ] + [ 6π r η v ]
Using eqn.(1) , above expression is rewritten as
[ 2 e E ] + [ (4/3) π r3 ρair g ] = [ 6π r η v ]
LHS = [ 2 × 1.602 × 10-19 × 105 ] + [ (4/3) π × ( 1.516 × 10-6 )3 × 1.293 × 9.8 ]
LHS = 3.222 × 10-14
v = ( 3.222 × 10-14 ) / ( 6π × 1.516 × 10-6 × 1.8 × 10-5 ) ≈ 9.5 × 10-5 m/s
Answered by Thiyagarajan K | 01 Apr, 2022, 09:44: AM
Concept Videos
-
All about electric fields
Define electric field in terms of Coulomb's force. Apply superposition prin... -
Electric Field - Part 2
This video explains the electric field due to a point charge and due to a s... -
Electric Field
Define electric field in terms of Coulomb's force. Apply superposition pri...
CBSE 12-science - Physics
Asked by srishtijha944 | 15 Jul, 2022, 09:55: PM
ANSWERED BY EXPERTCBSE 12-science - Physics
Asked by marshelojigas | 28 Jun, 2022, 06:46: AM
ANSWERED BY EXPERTCBSE 12-science - Physics
Asked by arjunsah797 | 01 Apr, 2022, 07:31: AM
ANSWERED BY EXPERTCBSE 12-science - Physics
Asked by arjunsah797 | 18 Mar, 2022, 12:06: PM
ANSWERED BY EXPERTCBSE 12-science - Physics
Asked by arjunsah797 | 15 Mar, 2022, 09:58: AM
ANSWERED BY EXPERTCBSE 12-science - Physics
Asked by vedhachethan | 19 Sep, 2021, 01:20: PM
ANSWERED BY EXPERTCBSE 12-science - Physics
Asked by avaneesh1162 | 14 Jun, 2021, 08:03: AM
ANSWERED BY EXPERTCBSE 12-science - Physics
Asked by avaneesh1162 | 13 Jun, 2021, 08:56: AM
ANSWERED BY EXPERTCBSE 12-science - Physics
Asked by ruchiaggarwal083 | 12 May, 2021, 08:47: AM
ANSWERED BY EXPERT
