CBSE Class 10 Answered
Let alpha and beta are the zeroes of a quadratic polynomial 2x²-5x-6 then form a quadratic polynomial whose zeroes are alpha+beta and alpha×beta
Asked by geetayadav18081983 | 15 Jun, 2022, 13:19: PM
Given quadratic equation is
f(x) = 2x2 -5x - 6
roots of above quadratic equation are 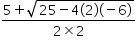 and
and 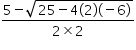
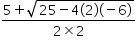 and
and 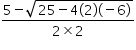
roots of above quadratic equation are 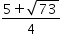 and
and 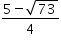
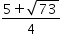 and
and 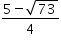
Hence 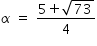 and
and 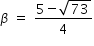
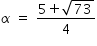 and
and 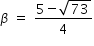
If roots of a quadratic equition are (α + β ) and ( α β ) , then quadratic equation is
g(x) = x2 - (α + β + α β ) x + (α + β ) ( α β )
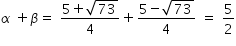
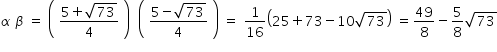
Hence quadratic equation is
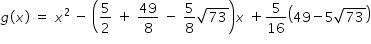
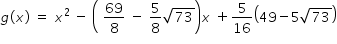
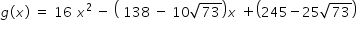
Answered by Thiyagarajan K | 15 Jun, 2022, 14:43: PM
Application Videos
Concept Videos
CBSE 10 - Maths
Asked by geetayadav18081983 | 15 Jun, 2022, 13:19: PM
CBSE 10 - Maths
Asked by kritikarautela16.8cpsb | 08 Apr, 2022, 22:07: PM
CBSE 10 - Maths
Asked by mahimakumari9777 | 31 Jul, 2020, 18:58: PM
CBSE 10 - Maths
Asked by sasmita7656 | 11 Jul, 2020, 17:22: PM
CBSE 10 - Maths
Asked by arajeevshashank | 25 Jun, 2020, 19:19: PM
CBSE 10 - Maths
Asked by Kumaaragururamakrishnan | 28 Mar, 2020, 20:33: PM
CBSE 10 - Maths
Asked by sg1929771 | 04 Jan, 2020, 19:24: PM