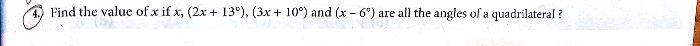CBSE Class 8 Answered
In the adjacent figure, ABCD is a parallelogram and line segments AE and CF bisect the angles A and C respectively. Show that AE||CF.
Asked by seemamehra1805 | 02 Sep, 2020, 13:57: PM
ABCD is a parallelogram with AE and CF being the bisectors of angles A and C respectively.

Answered by Renu Varma | 04 Sep, 2020, 14:23: PM
Application Videos
Concept Videos
CBSE 8 - Maths
Asked by rasal3771 | 24 Feb, 2023, 18:14: PM
CBSE 8 - Maths
Asked by antya2305 | 07 Jul, 2022, 21:56: PM
CBSE 8 - Maths
Asked by pramilam | 14 Feb, 2022, 16:52: PM
CBSE 8 - Maths
Asked by tanmaysinghrathore6 | 04 Aug, 2021, 19:46: PM
CBSE 8 - Maths
Asked by potphodenamita | 22 Sep, 2020, 20:17: PM
CBSE 8 - Maths
Asked by seemamehra1805 | 02 Sep, 2020, 13:57: PM
CBSE 8 - Maths
Asked by mokshithaanneboina | 26 Jun, 2020, 07:25: AM
CBSE 8 - Maths
Asked by armaanmeena1111 | 06 May, 2020, 14:46: PM
CBSE 8 - Maths
Asked by Kumarshourya90 | 08 Oct, 2019, 14:37: PM
CBSE 8 - Maths
Asked by Abhilashakharadkar53373 | 02 Jun, 2019, 11:02: AM