Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 11-science Answered

In how many ways can 5 girls and 3 boys be seated in a row so that no two boys are together?
Asked by Topperlearning User | 13 Sep, 2016, 02:58: AM
answered-by-expert Expert Answer

Let us first seat the 5 girls. This can be done in 5! Ways. For each such arrangement, the three boys can be seated only at the cross marked places.

                   GGGGG
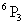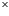
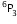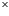
There are 6 cross marked place and the three boys can be seated in  ways. Hence, by multiplication principle, the total numbers of ways=5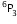!=14400
Answered by | 13 Sep, 2016, 04:58: AM

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 11-science - Maths
if npr-1/a=npr/b=npr+1/c then the value of b square/a(b+c)
Asked by tharshini8456157 | 27 Nov, 2023, 10:32: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
the number of words which can be formed out of the letters of the word PARTICLE so that vowels occupy even place is
Asked by ismayilpmamu | 09 Apr, 2020, 10:10: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
How many words can be formed by taking 4 letters at a time out of the letters of the words MATHEMATICS? 
Asked by Kashifimam866 | 20 Feb, 2019, 05:58: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
Find the no. Of arrangements  of the letters of the  word Delhi if e always  comes before i.
Asked by Sh1989kishore | 22 Oct, 2018, 10:12: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
From a group of 15 cricket players, a team of 11 players is to be chosen. In how many ways can this be done?
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
In how many ways can 5 girls and 3 boys be seated in a row so that no two boys are together?
Asked by Topperlearning User | 13 Sep, 2016, 02:58: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
In how many ways can 9 persons sit around a table so that all shall not have the same neighbours in any two arrangements?
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
How many triangles can be obtained by joining 12 points, five of which are collinear?
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
A student has to answer 10 questions, choosing at least 4 from each of part A and part B. If there are 6 questions in Part A and in part B, in how many ways can the student choose 10 questions?
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
If 8 parallel lines in a plane are intersected by a family of 10 parallel lines. Find the number of parallelograms formed?
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×