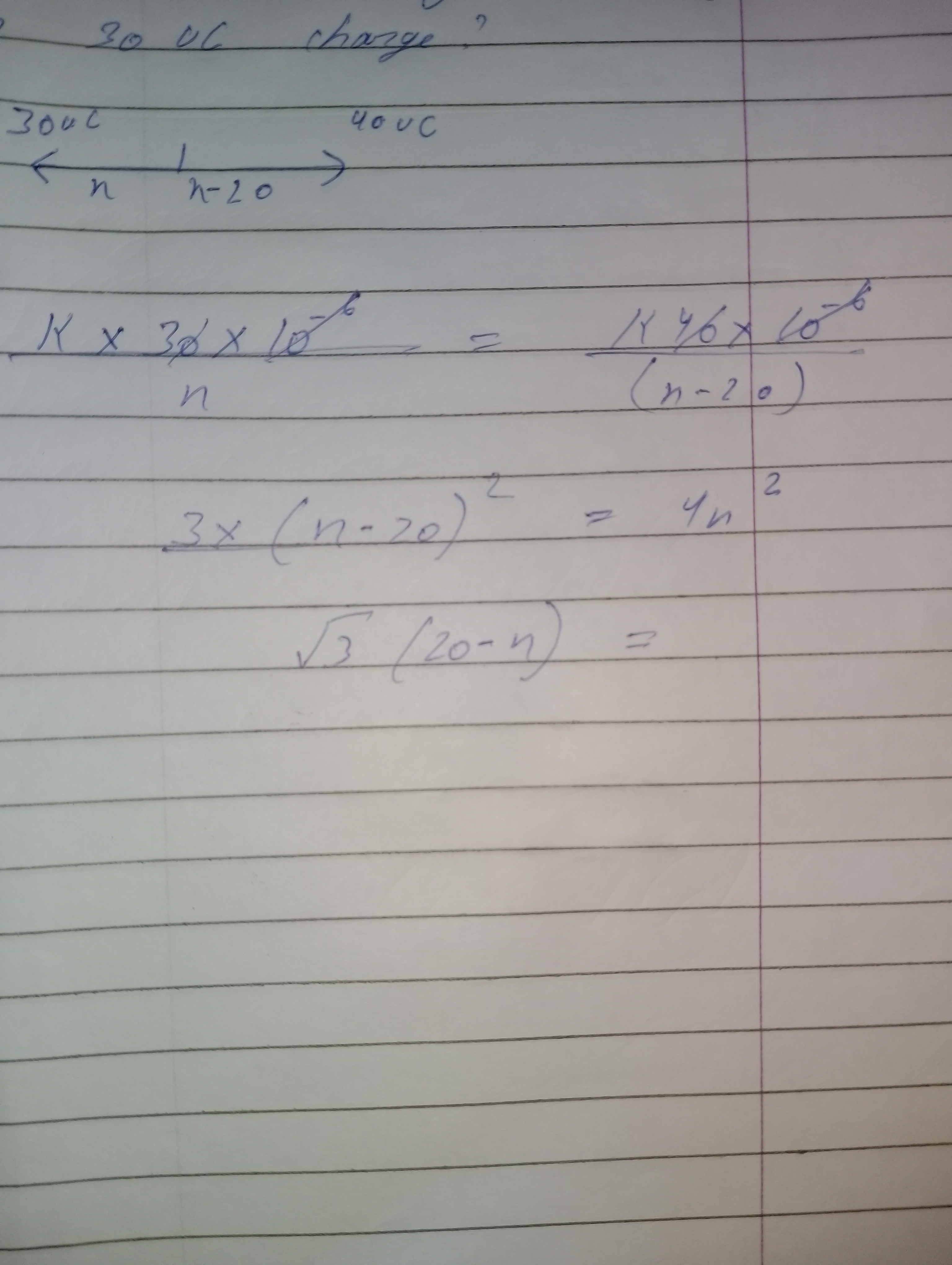Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 12-science Answered

In fig three point charges q,-2q are q are placed along the x axis. Show that the electric field at p along the y axis is E =(1/4×3.14×e knot)×(3qa^2/y^4),when y>>a.integral to the power of straight R to the power of straight y end exponent over blank
Asked by sharmashiva3667.12sdatl | 08 Jun, 2020, 08:32: PM
Expert Answer
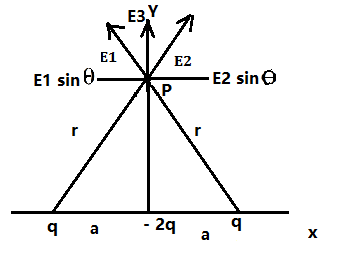
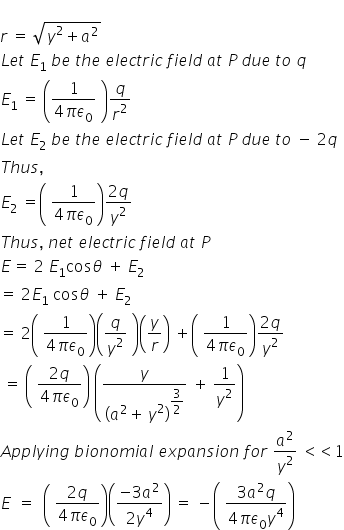
r space equals space square root of y squared plus a squared end root L e t space E subscript 1 space b e space t h e space e l e c t r i c space f i e l d space a t space P space d u e space t o space q space E subscript 1 space equals space open parentheses fraction numerator 1 over denominator 4 pi epsilon subscript 0 end fraction space close parentheses q over r squared space L e t space E subscript 2 space b e space t h e space e l e c t r i c space f i e l d space a t space P space d u e space t o space minus space 2 q space T h u s comma space E subscript 2 space equals open parentheses space fraction numerator 1 over denominator 4 pi epsilon subscript 0 end fraction close parentheses fraction numerator 2 q over denominator y squared end fraction space T h u s comma space n e t space e l e c t r i c space f i e l d space a t space P space E thin space equals space 2 space E subscript 1 cos theta space plus thin space E subscript 2 equals space 2 E subscript 1 space cos theta space plus thin space E subscript 2 space equals space 2 open parentheses space fraction numerator 1 over denominator 4 pi epsilon subscript 0 end fraction close parentheses open parentheses q over y squared space close parentheses open parentheses y over r close parentheses space plus open parentheses space fraction numerator 1 over denominator 4 pi epsilon subscript 0 end fraction close parentheses fraction numerator 2 q over denominator y squared end fraction space space equals space open parentheses space fraction numerator 2 q over denominator 4 pi epsilon subscript 0 end fraction close parentheses space open parentheses y over open parentheses a squared plus thin space y squared close parentheses to the power of begin display style 3 over 2 end style end exponent space plus thin space 1 over y squared close parentheses space A p p l y i n g space b i o n o m i a l space e x p a n s i o n space f o r space a squared over y squared space less than less than 1 E space space equals space space open parentheses space fraction numerator 2 q over denominator 4 pi epsilon subscript 0 end fraction close parentheses open parentheses fraction numerator negative 3 a squared over denominator 2 y to the power of 4 end fraction close parentheses space equals space minus open parentheses space fraction numerator 3 a squared q over denominator 4 pi epsilon subscript 0 y to the power of 4 end fraction close parentheses space
Answered by Shiwani Sawant | 09 Jun, 2020, 09:10: PM

Concept Videos

Multiple Choice Questions Practice Test Subjective Questions Webinar Subjective Questions Pre Board Assessment
Answered Unanswered My Questions My Answers
CBSE 12-science - Physics
an infinite line charge produces a field of 9×10^4 N/C at a distance of 2 cm calculate the linear charge
Asked by srishtijha944 | 15 Jul, 2022, 09:55: PM
ANSWERED BY EXPERT
CBSE 12-science - Physics
Three charges \( 1 \mathrm{C},-1 \mathrm{C} \), and \( 2 \mathrm{C} \) are kept on \( X \) axis \( -5 \mathrm{~cm}, x=0 \mathrm{~cm} \) amd \( x=10 \mathrm{~cm} \) respectively find net force one each of them
Asked by marshelojigas | 28 Jun, 2022, 06:46: AM
ANSWERED BY EXPERT
CBSE 12-science - Physics
ln a Millikan’s oil drop experiment, the horizontal plates are 1.5 cm apart. With the electric field switch off an oil drop is observed to fall with a steady velocity of 2.5×10^{-2}  cm  s^{-1}.  When the field is switched on the upper plate being positive, the drop just remains stationary when the   p.d.   between the plates is 1500 V. Calculate the radius of drop (b) How many electronic charges does it carry? (c)If the   p.d. between the two plates remains unchanged, with what velocity will the drop move when it has collected two more as a result of exposure to ionising radiation? (Oil density, rho=900 kgm^{3} , Viscosity of air,   eta =1.8×10^{-5} Nsm^{-2}, Density of air,  σ=1.293  kg  m^{-3})
Asked by arjunsah797 | 01 Apr, 2022, 07:31: AM
ANSWERED BY EXPERT
CBSE 12-science - Physics
A beam of electrons, moving with avelocity of 10^7m/s, enters midway between two horizontal parallel plates in a directions parallel to the plates. Each plate is 5 cm long. These plates are kept 2 cm apart and a potential difference of 90 V is applied between, them. Calculate the velocity of the electron- beam with which it just grazes the edge of the positive plate. (e  /m=1.8×10^{11}  c/kg)
Asked by arjunsah797 | 18 Mar, 2022, 12:06: PM
ANSWERED BY EXPERT
CBSE 12-science - Physics
An oil drop of mass 3.25*10^(-15) kg falls vertically with uniform velocity , through the air between vertical parallel plates which are 2 m apart. When a p.d. of 1000 V is applied to the plates the drop moves to the positively charged plate , being inclined at 45 degrees to the vertical. Calculate the charge on the drop. 
Asked by arjunsah797 | 15 Mar, 2022, 09:58: AM
ANSWERED BY EXPERT
CBSE 12-science - Physics
Two point charges 2 C and 3 uC are placed at two comers of an equilateral triangle of side 20 cm in free space. Calculate the magnitude of resultant electric field at the third corner of the triangle. If an & - particle is placed at the third corner, what is the force acting on it? (Charge on & – particle is 3.2 x 10-19 €).
Asked by vedhachethan | 19 Sep, 2021, 01:20: PM
ANSWERED BY EXPERT
CBSE 12-science - Physics
Asked by avaneesh1162 | 14 Jun, 2021, 08:03: AM
ANSWERED BY EXPERT
CBSE 12-science - Physics
State Gauss's theorem ? Derive the expression for electric field due Spherical hollow conductor and infinitely charged sheet and linearly charged conductors.
Asked by avaneesh1162 | 13 Jun, 2021, 08:56: AM
ANSWERED BY EXPERT
CBSE 12-science - Physics
A simple pendulum is having bob of mass m carrying a charge q and is hanging from ceiling. A uniform electric field E is applied in downward direction then time period of simple pendulum is.
Asked by ruchiaggarwal083 | 12 May, 2021, 08:47: AM
ANSWERED BY EXPERT
CBSE 12-science - Physics
An electric field E is applied between the plates a and b as shown in the figure a charge particle of mass m and charge q is projected along the direction as shown fig it's velocity v find vertical distance y covered by the partical when goes out of the electric field region
Asked by arorarajaryan2003 | 28 Apr, 2021, 10:11: PM
ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get FREE Sample Mock Papers for Final Exams
Download Now
×