CBSE Class 10 Answered
in fig. DEparallelCA and D is a point on BC such that BD/DC=2/3.the ratio of area of triangle ABC to area of triangle BDE is
Asked by deepika babbar | 23 Sep, 2013, 06:30: PM
DE is parallel to CA
So, angle BDE = angle BCA
angle BED = angle BAC
Hence, triangles BDE and BCA are similar (by AA similarity)
We know that the ratio of areas of two similar triangles is equal to the ratio of the squares of their corresponding sides.
So,
ar (ABC) / ar(EBD) = BC2 / BD2 ... (1)
Given, BD / DC = 2/3
So, BD/BD+DC = 2/2+3
This gives BD/BC = 2/5
From (1),
ar (ABC) / ar(EBD) = 52 / 22 = 25/4
Answered by | 23 Sep, 2013, 10:08: PM
Application Videos
Concept Videos
CBSE 10 - Maths
Asked by suryapalsinghgoudmahirajbanna | 17 Sep, 2023, 10:50: PM
CBSE 10 - Maths
Asked by bnarayanamstr | 03 May, 2023, 10:03: AM
CBSE 10 - Maths
Asked by savitamahajan202 | 30 Dec, 2022, 12:51: PM
CBSE 10 - Maths
Asked by bhu.joshi54 | 04 Jul, 2022, 08:18: PM
CBSE 10 - Maths
Asked by bhu.joshi54 | 16 Jun, 2022, 07:56: PM
CBSE 10 - Maths
Asked by dishapalnati82 | 24 Nov, 2021, 09:30: AM
CBSE 10 - Maths
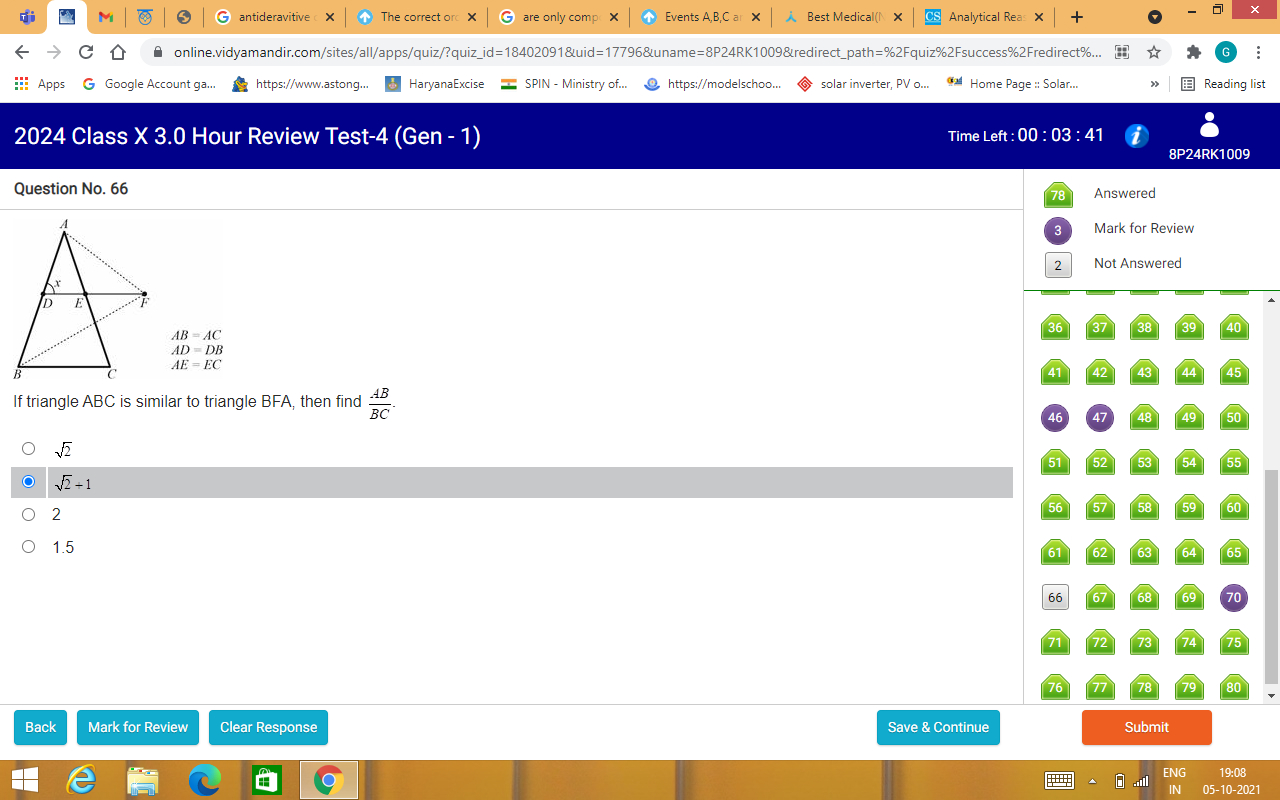
Asked by psinghaladv | 05 Oct, 2021, 07:49: PM