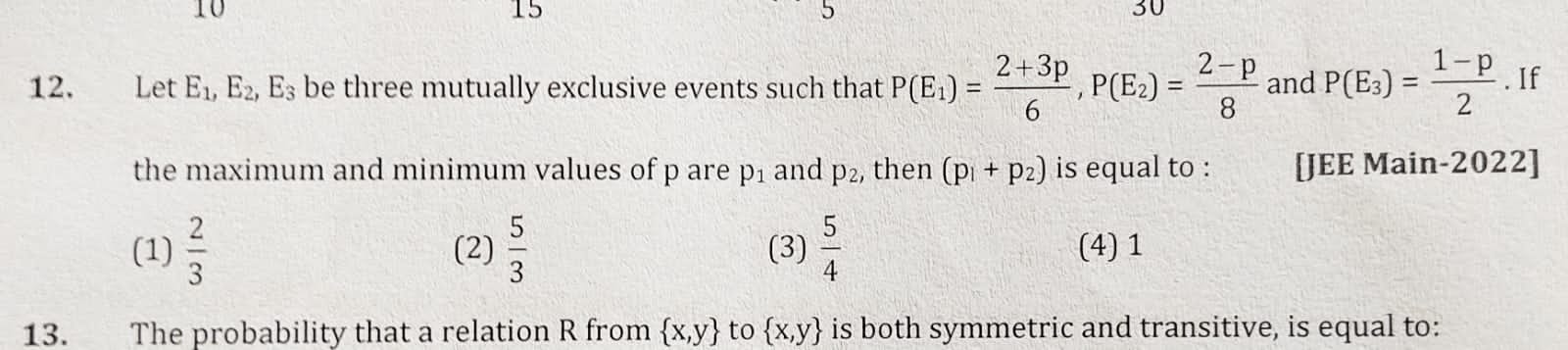Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 12-science Answered

In answering a question on a multiple choice test,a student either knows the answer or guesses .Let 3/4 be the probabillity that he knows the answer and 1/4 be the probability that he guesses.Assuming that a student who guesses at the answer will be correct with probability 1/4.what is the probability that the student knows the answer given that he answered it correctly?
Asked by DIPTI PRIYA | 16 Mar, 2011, 12:00: AM
answered-by-expert Expert Answer
Dear Student,
Here is the solution:
let E be the event where the student gets the answer right, this can be the result of 2 separate events
E1- he knows the answers hence marks it correct
E2- he guesses and gets it correct

if E1 happens then the prob that he gets it correct P(E|E1)= 1
given P(E1)= 3/4

if E2 happens then the prob that he gets it correct P(E|E2)= 1\4
given P(E2)= 1\4

using baye's theorem
P(E1|E)= P(E|E1) x P(E1)/( P(E1) P(E|E1) +P(E2)P(E|E2) )
=(1 x 3/4)/( 3/4 x 1 + 1/4 x 1/4)
=12/13
Hope this helps!

Regards
Team Topperlearning.
Answered by | 16 Mar, 2011, 07:37: AM

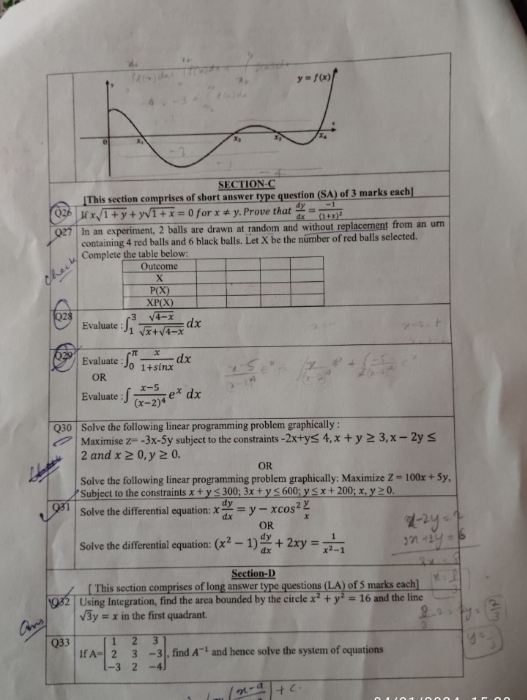
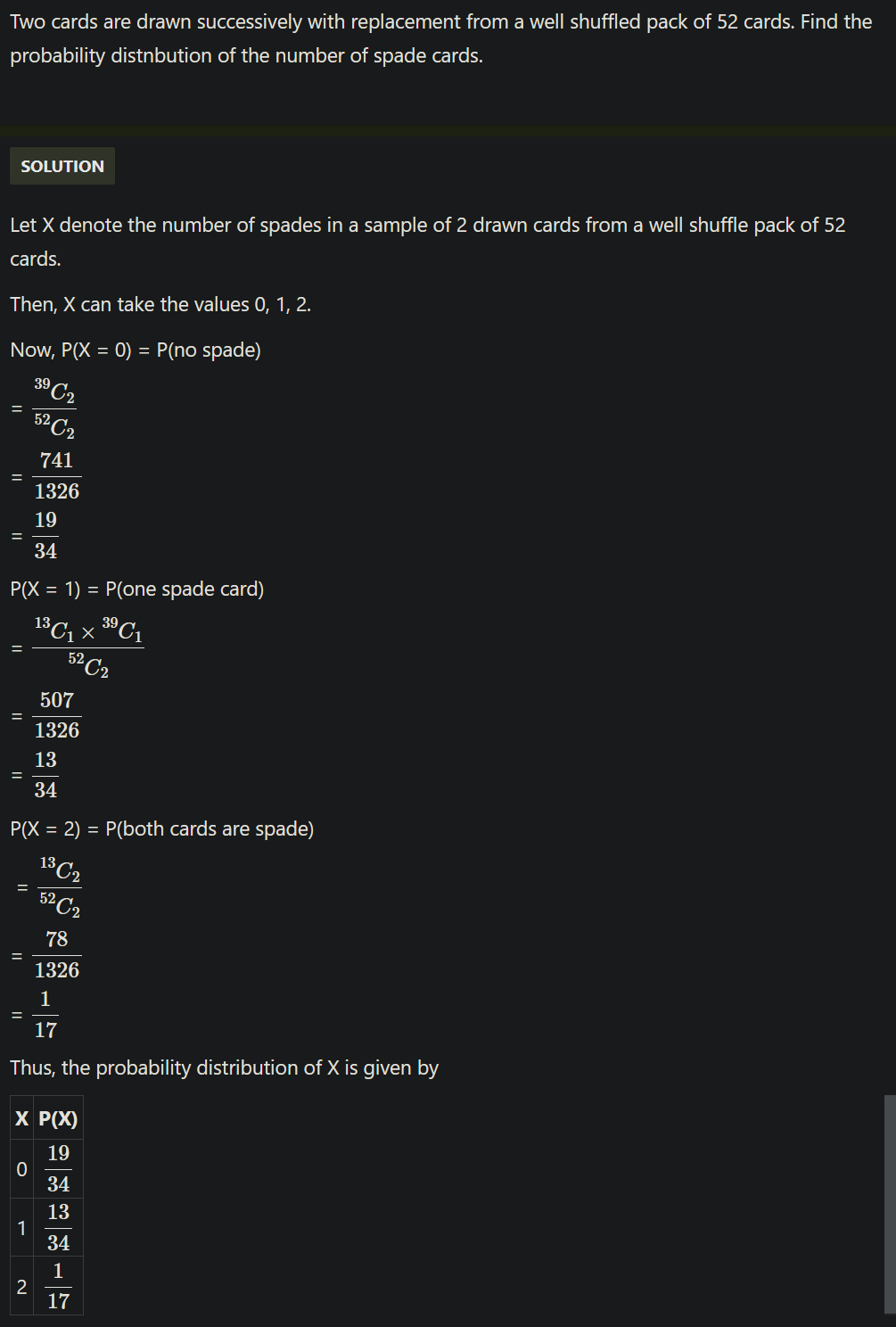
Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 12-science - Maths
The probability that a pen manufactured by a company will be defective is 0.1. If 12 such pens are selected find the probability that i) exactly 2 will be detective ii) at least 2.will be defective iii)none will he defective
Asked by annapoornaa429 | 31 Mar, 2024, 08:23: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
bag 1 contains 8 red and 2 black balls. bag 2 contains 7 red and 5 Black balls. one of the bags is chosen at random and a ball is drawn from it, which is found to be black. find the probability that the ball is drawn from bag 1.
Asked by janusingh736 | 13 Mar, 2024, 04:19: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Q27 Check In an experiment, 2 balls are drawn containing 4 red balls and 6 black balls. Let X be the number of red balls selected. Complete the table below: Outcome overline P(X) XP(X)
question image
Asked by khushisjkvm | 04 Jan, 2024, 07:14: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
the question and the solution is in the attachment, can you explain how can they use combinations when combinations does not account for replacement while it is mentioned in the question that replacement is to be taken into account? And can you provide the correct answer.
question image
Asked by ashwinskrishna2006 | 26 Dec, 2023, 07:34: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
doubt
question image
Asked by armaanjain840 | 20 Dec, 2023, 05:59: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Two urns contains 1 white,6 red and 4 white,3 red balls. One of t 3 he urn is selected at random and a ball is drawn from it. Find: (1) The probability of drawing a red ball. (ii) The probability of drawing the ball from the first urn if b all drawn is red.
Asked by babitdevi283 | 14 Nov, 2023, 09:42: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
4. The probability that a visitor in the dining room will need the first course is equal to 0.8.  Find the probability that out of 100 visitors, no less than 75 and no more than 90 visitors will order the first dish.
Asked by surajsharmaisonline | 20 Jan, 2023, 12:28: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Assuming the probability of a male birth as 1/2, find the probability that a family of 3 children will have: a) two boys and one girl b) at most two girls 
Asked by arjunsah797 | 03 May, 2022, 10:04: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
A Five digits number is written down at random. Find the probability that number is divisible by 5 and no two consecutive digits are identical.
Asked by rairp2017 | 27 May, 2021, 12:21: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Find the probability of success p for a binomial distribution, if n = 6 and 4 × P(X=4) = P(X=2)
Asked by 1999shaileshraj | 22 Feb, 2020, 11:50: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×