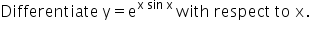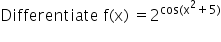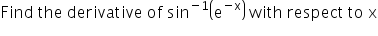Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 12-science Answered

If e^x +e^y  =e^x+y Then prove         dy/dx  + e^y-x =0
Asked by iasaspirant20s | 09 Oct, 2022, 02:31: PM
answered-by-expert Expert Answer
e^x + e^y = e^x+y
Differentiating w.r.t x, we get
e^x + e^y dy/dx = e^x+y (1 + dy/dx)
dy/dx (e^y - e^x+y) = e^x+y - e^x
dy/dx = (1 - e^-y)/(e^-x - 1)
Answered by Renu Varma | 20 Oct, 2022, 09:21: AM

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 12-science - Maths
If e^x +e^y  =e^x+y Then prove         dy/dx  + e^y-x =0
Asked by iasaspirant20s | 09 Oct, 2022, 02:31: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
if y=x^2 e^ax,then find y n term.
Asked by ashchutiaok | 17 Mar, 2022, 10:42: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Find the derivatives of the function w.r.t X  Y = 5^logsinx +(Sinx)^x
Asked by evanbose3 | 05 Jul, 2019, 10:28: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
 Differentiate wrt x xlog x
Asked by haroonrashidgkp | 03 Jun, 2018, 11:24: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Differentiate space straight y equals straight e to the power of straight x space sin space straight x end exponent space with space respect space to space straight x.
Asked by Topperlearning User | 01 Aug, 2014, 12:21: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
  Differentiate space straight f left parenthesis straight x right parenthesis space equals 2 to the power of cos left parenthesis straight x squared plus 5 right parenthesis end exponent
Asked by Topperlearning User | 01 Aug, 2014, 12:36: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Find space the space derivative space of space straight y equals log subscript 2 open parentheses log subscript 2 straight x close parentheses
Asked by Topperlearning User | 01 Aug, 2014, 12:40: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Differentiate space straight y equals straight a to the power of left parenthesis tan to the power of minus 1 end exponent straight x right parenthesis squared end exponent
Asked by Topperlearning User | 01 Aug, 2014, 12:42: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
  Find space the space derivative space of space sin to the power of minus 1 end exponent open parentheses straight e to the power of minus straight x end exponent close parentheses space with space respect space to space straight x
Asked by Topperlearning User | 01 Aug, 2014, 12:45: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Find space the space derivative space of space straight e to the power of straight e to the power of straight x end exponent.
Asked by Topperlearning User | 01 Aug, 2014, 12:48: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×