CBSE Class 12-science Answered

The motion of the electron is not free. The electron is bound to the atom by the attractive force of the nucleus and consequently quantum mechanics predicts that the total energy of the electron is quantized. The expression for the energy is: 

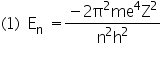n=1,2,3,4,.....

where m is the mass of the electron, e is the magnitude of the electronic charge, n is a quantum number, h is Planck's constant and Z is the atomic number (the number of positive charges in the nucleus)

This formula applies to any one-electron atom or ion. For example, 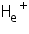  is a one-electron system for which Z=2.

 As in our previous example, we shall represent all the constants which appear in the expression for E_n by a constant K and we shall set Z = 1. 

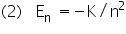n = 1,2,3,....

Since the motion of the electron occurs in three dimensions we might correctly anticipate three quantum numbers for the hydrogen atom. But the energy depends only on the quantum number n and for this reason it is called the principal quantum number. In this case, the energy is inversly dependent upon n², and as n is increased the energy becomes less negative with the spacings between the energy levels decreasing in size. When n = ¥ , E  = 0 and the electron is free of the attractive force of the nucleus.  The average distance between the nucleus and the electron (the average value of r) increases as the energy or the value of n increases. Thus energy  must be supplied to pull the electron away from the nucleus.

    The parallelism between increasing energy and increasing average value of r is a useful one. In fact, when an electron loses energy, we refer to it  as "falling" from one energy level to a lower one on the energy level diagram. Since the average distance between the nucleus and the electron also decreases with a decrease in n, then the electron literally does fall in closer to the nucleus when it "falls" from level to level on the energy level diagram.

  The energy difference between E_¥ and E₁: 

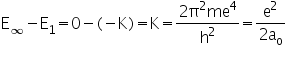is called the ionization energy. It is the energy required to pull the electron completely away from the nucleus and is, therefore, the energy of the reaction: 

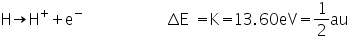This amount of energy is sufficient to separate the electron from the attractive influence of the nucleus and leave both particles at rest. If an amount of energy greater than K is supplied to the electron, it will not only escape from the atom but the energy in excess of K will appear as kinetic energy of the electron. Once the electron is free it may have any energy because all  velocities are then possible.