Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 11-science Answered

For any real x find the minimum and maximum value for the expression 3sin^2x +3sinxcosx + 7cos^2x.
Asked by acv27joy | 10 Dec, 2018, 13:10: PM
answered-by-expert Expert Answer
3sin2x +3sinxcosx + 7cos2x
Use cos2x = 1 - 2sin2x = 2cos2 x - 1
sin2x = 2sinxcosx
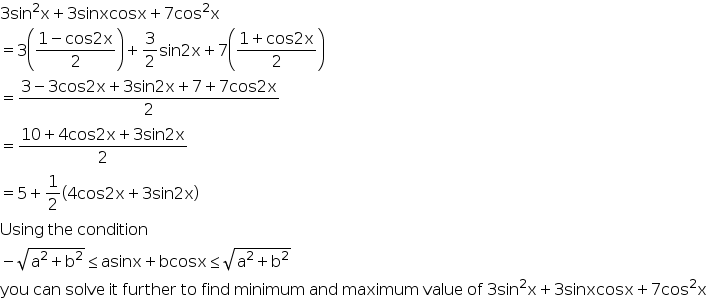
begin mathsize 16px style 3 sin squared straight x plus 3 sinxcosx plus 7 cos squared straight x equals 3 open parentheses fraction numerator 1 minus cos 2 straight x over denominator 2 end fraction close parentheses plus 3 over 2 sin 2 straight x plus 7 open parentheses fraction numerator 1 plus cos 2 straight x over denominator 2 end fraction close parentheses equals fraction numerator 3 minus 3 cos 2 straight x plus 3 sin 2 straight x plus 7 plus 7 cos 2 straight x over denominator 2 end fraction equals fraction numerator 10 plus 4 cos 2 straight x plus 3 sin 2 straight x over denominator 2 end fraction equals 5 plus 1 half open parentheses 4 cos 2 straight x plus 3 sin 2 straight x close parentheses Using space the space condition minus square root of straight a squared plus straight b squared end root less or equal than asinx plus bcosx less or equal than square root of straight a squared plus straight b squared end root you space can space solve space it space further space to space find space minimum space and space maximum space value space of space 3 sin squared straight x plus 3 sinxcosx plus 7 cos squared straight x end style 
Answered by Sneha shidid | 12 Dec, 2018, 09:49: AM

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 11-science - Maths
Prove that 2sin^2 y + 4cos(x + y) sinxsiny ny + cos 2 * (x + y) = cos 2x
Asked by apnp31 | 21 Sep, 2020, 12:19: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
Cos5π/4-sin5π/4+tan11π/4-cot11π/4? SIn4530°? Cos (-9π/4)? Sin 120°cos 150°-cos240°sin330°? If tan35°=k then,Tan145°-Tan125°/1+Tan145°.Tan125°?
Asked by Pallapothu.a | 05 Aug, 2020, 16:13: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
clear my doubt
question image
Asked by kandukuriPraneeth16 | 25 Jul, 2020, 18:18: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
trigonometry ka question hai please solve
question image
Asked by jaiswalpiyush040 | 20 Jul, 2020, 08:22: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
Prove that cos^2 pi/8 + cos^2 3pi/8 + cos^2 5pi/8 + cos^2 7pi/8 =2  
Asked by anushkapanwar74 | 15 Aug, 2019, 13:26: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
2 tan B + cot B = tan A , show that 2 tan(A-B) = cot B
Asked by agarwalharsh8476 | 06 Aug, 2019, 20:32: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
sinx1sinx2-cosx1cosx2+1=0 the value of tanx1/2*tanx2/2 is alwya equal to?  
Asked by aahnik.mohanty | 29 May, 2019, 20:00: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
For any real x find the minimum and maximum value for the expression 3sin^2x +3sinxcosx + 7cos^2x.
Asked by acv27joy | 10 Dec, 2018, 13:10: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
If sin x + cos x = sqrt{y+(1/y)} such that x belongs to [0,6Π] and y>0 prove that x = Π/4 or 9Π/4.
Asked by acv27joy | 08 Oct, 2018, 09:42: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
(sinø-cosø)^2=1-sin2ø
Asked by abhaysharma2710 | 15 Jul, 2018, 10:09: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt