CBSE Class 11-science Answered
For any natural number n, Prove that
.
.
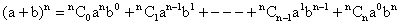Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
Expert Answer
The proof is obtainted by applying principle of mathematical induction.
Let the given statement be
P(n):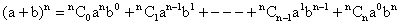 
For n = 1, we have
P(1) :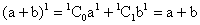 
Thus P(1) is true.
Suppose P(k) is true for some positive integer k, i.e.
(1)We shall prove that P(k+1) is also true, i.e.
Now,
= (a+b) 
[From (1)]
(By actual multiplication)
[grouping like terms]
Thus, it has been proved that P(k +1) is true whenever P(k) is true.
By principle of mathematical induction, P(n) is true for every positive integer n.
Answered by | 04 Jun, 2014, 03:23: PM
Concept Videos
-
Binomial Theorem for Positive Index
This video covers examples and concepts related to Binomial Theorem for the... -
Binomial Theorem for Positive Index
This video covers examples and concepts related to Binomial Theorem for the... -
Quick revision on Binomial theorem for positive index ...
State the Binomial Theorem for the positive Index and explore properties of...
CBSE 11-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
ANSWERED BY EXPERTCBSE 11-science - Maths
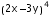by using binomial expansion.Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
ANSWERED BY EXPERTCBSE 11-science - Maths
.Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
ANSWERED BY EXPERTCBSE 11-science - Maths
: Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
ANSWERED BY EXPERTCBSE 11-science - Maths
: Asked by Topperlearning User | 30 Sep, 2016, 09:11: PM
ANSWERED BY EXPERTCBSE 11-science - Maths
.Asked by Topperlearning User | 30 Sep, 2016, 09:15: PM
ANSWERED BY EXPERTCBSE 11-science - Maths
:Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
ANSWERED BY EXPERT
