Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 10 Answered

Find the sum of the first 17 term of an AP whose 4th term = -15 and 9th term = -30.
Asked by arindeep.singh | 26 Jun, 2020, 03:34: PM
answered-by-expert Expert Answer
4th term = -15 and 9th term = -90
a + 3d = -15 ... (i) and
a + 8d = -30 ... (ii)
Subtracting (ii) from (ii), we get
5d = -15
d = -3
Substituting the value of d in (i), we get
a + 3(-3) = -15
a - 9 = -15
a = -6
Sum of n terms if given by
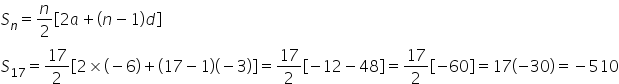
S subscript n equals n over 2 open square brackets 2 a plus left parenthesis n minus 1 right parenthesis d close square brackets S subscript 17 equals 17 over 2 open square brackets 2 cross times left parenthesis negative 6 right parenthesis plus left parenthesis 17 minus 1 right parenthesis left parenthesis negative 3 right parenthesis close square brackets equals 17 over 2 open square brackets negative 12 minus 48 close square brackets equals 17 over 2 open square brackets negative 60 close square brackets equals 17 open parentheses negative 30 close parentheses equals negative 510
Answered by Renu Varma | 28 Jun, 2020, 05:14: PM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 10 - Maths
find the sum of following 6+13+20+....+97
Asked by deepikaselvam2009 | 20 Feb, 2024, 08:57: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
If the sum of the first n terms of an AP be n and the sum of first n terms be m then sum of its (m+n) terms is -(m+n)
Asked by keshavsinghalhapur | 16 Jan, 2024, 08:46: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
If the sum of first n,2n and 3n terms of an AP be S1 S2andS3 respectively then p3 S2-S1
Asked by keshavsinghalhapur | 15 Jan, 2024, 10:56: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
A contract on construction job specifies penalty for delay of completion beyond a certain date as follows Rs. 200 for 1st, Rs. 250 for 2nd, and Rs. 300 for 3rd, so on. If contractor pays Rs. 27,750 as penalty, find the number of days for construction work delayed.
Asked by skandachiranjeevin | 06 Dec, 2023, 07:08: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
The sum of the first 7 terms of an AP is 63 and that of its next 7 terms is 161.find the AP
Asked by prassanna.j | 13 Nov, 2023, 11:24: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
If the pth term of an AP is 1/q and qth term 1/P. Prove that the sum of the first pqth term is 1/2 (pq + 1).
Asked by latayadav23 | 17 Oct, 2023, 08:39: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
if in an A.P. the sum of m terms equal to n and the sum of n terms is equal to m, then prove that the sum of (m+n) terms is -(m+n)
Asked by ananya_monica | 28 Sep, 2023, 07:07: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
find the sum of 8 multiple of 1.5
Asked by simmysingh1aug | 20 Sep, 2023, 10:20: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
find the sum of first 51 term of an AP whose second and third terms are 14 and 18 respectively.
Asked by bkhaiwangkonyak | 07 Mar, 2023, 04:35: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
the sum of fourth and eight terms of an A.P is 54 and their product is 665. find the sum of the first thirty terms of an A.P​
question image
Asked by sakshinde95 | 23 Jan, 2023, 05:50: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×