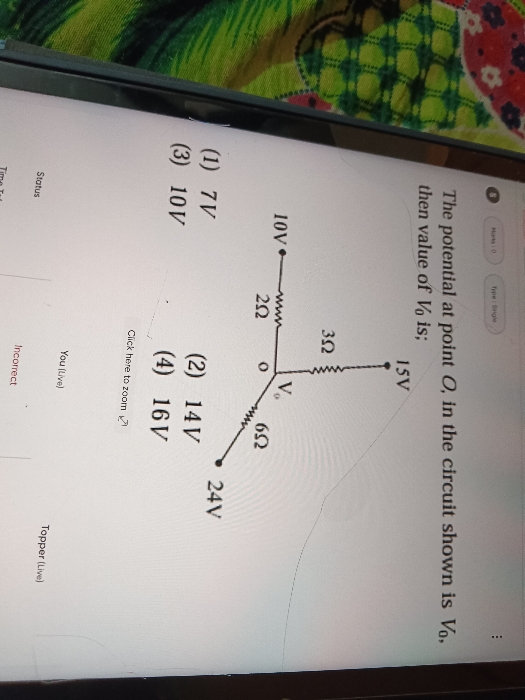
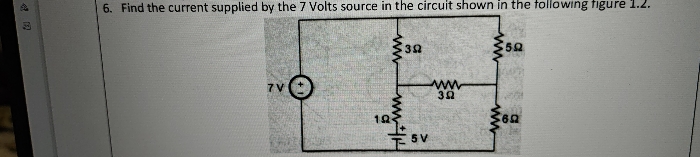
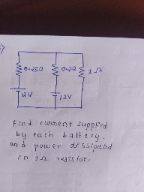
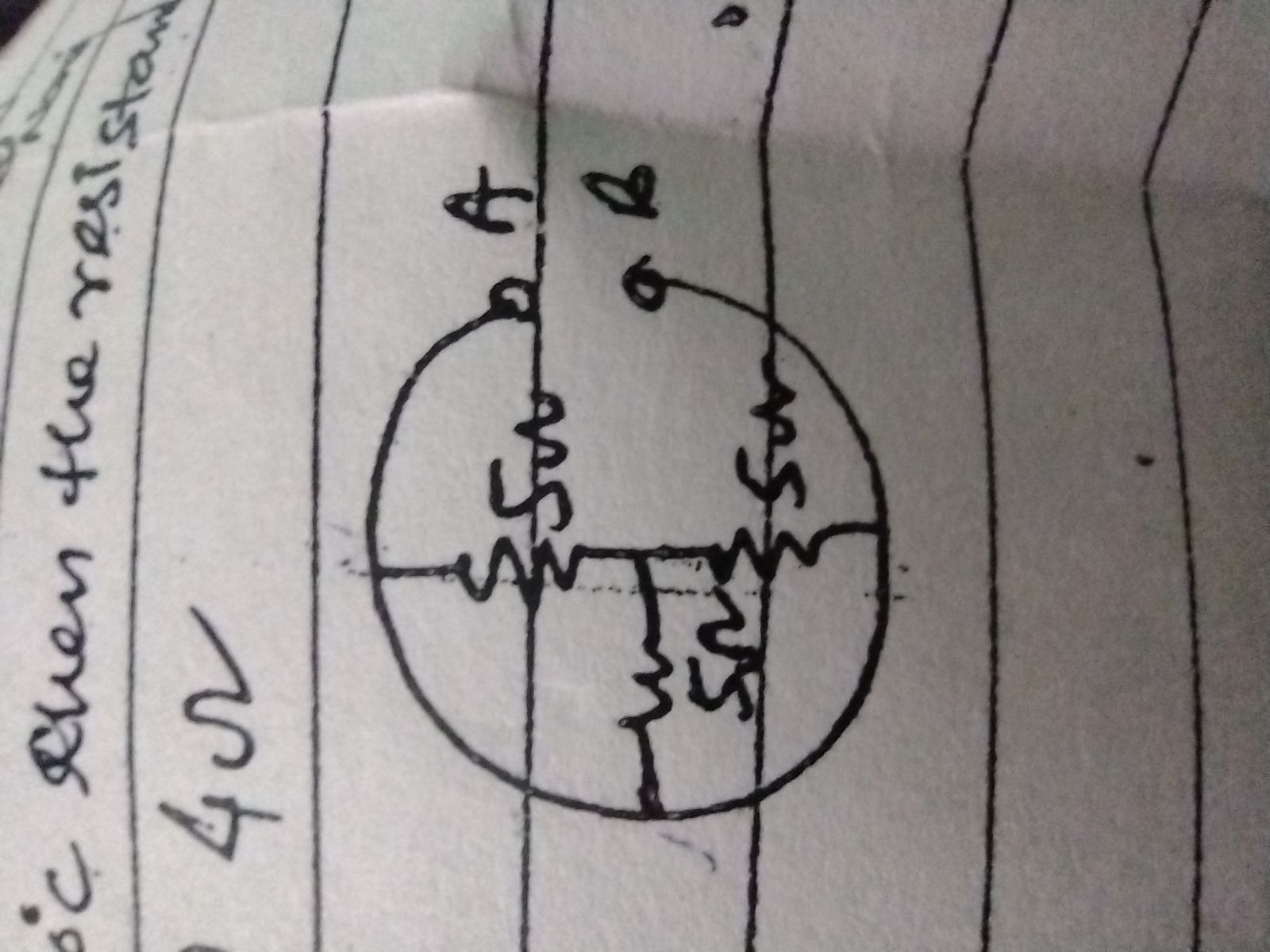
CBSE Class 12-science Answered
BELOW
Asked by www1028 | 07 Jul, 2010, 07:25: PM
Expert Answer
We know that resistance is given by, R = ρxL/A
Lets take its inital diameter to be 'd' and initial lenght as 'l', therefore we get
A = pi (d/2)2 = pixd2/4
R = ρxl/A
= ρxl/(pixd2/4)
= 4ρxl/pixd2
Now its given that the new diameter is half of the inital diameter,
ie, d' = d/2
Therefore new A' = pix(d'/2)2 = pix(d/2x2)2 = pix(d/4)2 = pixd2 /16 = A/4
Now to find out the new length of the wire we will apply mass conservation,
ie, Mass after elongation = Mass before elongation
Mass after elongation =σ A' l'
Mass after elongation =σ A l
where,
σ = Density of the wire
l' = new length of the wire after elongation
σ A' l' = σ A l
therefore, l' = Axl/A'
= pix(d2/4)xl/pix(d2/16)
= 4l
Now putting value of A' and l', for getting the value of new resistance R', we get
R' = ρxl'/A'
= ρx(4l)/(A/4)
= (4x4) [(ρxl/A)]
= (16) (R)
hence, R' = 16R.
Hope this helps.
Team Topper
Answered by | 12 Jul, 2010, 04:02: PM
Concept Videos
-
Electric Current
This video explains the concept of electric current. -
Drift of Electrons - Part 1
This video explain the drift speed and its dependence on the externally app... -
Compare the resistivity of conductors, insulators and s ...
Compare the resistivity of conductors, insulators and semiconductors. Study... -
About emf, potential difference & internal resistan ...
Define emf, potential difference & internal resistance. Identify factors on... -
Combination of Cells - Part 1
This video describes about the working of cells in series combination.
CBSE 12-science - Physics
Asked by heymindurownbusiness | 04 May, 2024, 11:15: AM
ANSWERED BY EXPERTCBSE 12-science - Physics
Asked by mailtoanjalip2005 | 16 Mar, 2024, 08:22: PM
ANSWERED BY EXPERTCBSE 12-science - Physics
Asked by patelnamra608 | 26 Jan, 2024, 11:01: AM
ANSWERED BY EXPERTCBSE 12-science - Physics
Asked by smitdholakiya28 | 17 Dec, 2023, 09:37: AM
ANSWERED BY EXPERTCBSE 12-science - Physics
Asked by shivashikhar69 | 09 Dec, 2023, 02:27: PM
ANSWERED BY EXPERTCBSE 12-science - Physics
Asked by nikhilsai2616 | 19 Nov, 2023, 01:05: AM
ANSWERED BY EXPERTCBSE 12-science - Physics
Asked by snehashiragannavar773 | 21 Oct, 2023, 02:38: PM
ANSWERED BY EXPERTCBSE 12-science - Physics
Asked by dr.strange45678 | 02 Aug, 2023, 12:31: PM
ANSWERED BY EXPERTCBSE 12-science - Physics
Asked by komalbrar0987 | 17 May, 2023, 06:15: PM
ANSWERED BY EXPERT
