CBSE Class 10 Answered
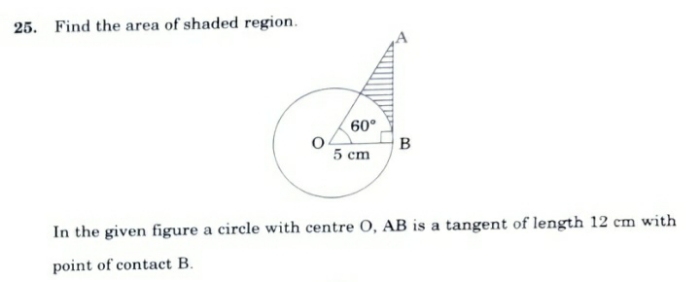
AB is a chord of length 24cm of a circle of radius 13cm. The tangents at A and B intersect at C. Find the length AC.
Asked by yashjain | 28 Nov, 2012, 04:13: PM
Expert Answer
Join Centre O with C and this line will be perpendicular bisector of AB.
Therefor AD=DB=12
OB=13
Therefor OD^2=(OB)^2-(DB)^2=25
Therefor OD=5
Let Angle ODB=X
In triangle ODB, tan X=DB/DO=12/5
In triangle OCB, tan X=CB/BO=CB/13
Equating both values of tan X
12/5=CB/13
Therefor CB=(12*13)/5=156/5=31.2
Answered by | 29 Nov, 2012, 11:59: PM
CBSE 10 - Maths
Asked by sheetal.kolte | 15 Mar, 2024, 03:25: PM
ANSWERED BY EXPERT
CBSE 10 - Maths
Asked by mp2235793 | 11 Jan, 2024, 10:31: PM
ANSWERED BY EXPERTCBSE 10 - Maths
Asked by lakshmimanjula433 | 19 Nov, 2023, 10:50: AM
ANSWERED BY EXPERTCBSE 10 - Maths
Asked by latayadav23 | 14 Oct, 2023, 12:49: PM
ANSWERED BY EXPERTCBSE 10 - Maths
Asked by latayadav23 | 14 Oct, 2023, 12:19: PM
ANSWERED BY EXPERTCBSE 10 - Maths
Asked by paresh0311 | 18 Mar, 2023, 10:58: PM
ANSWERED BY EXPERT
CBSE 10 - Maths
Asked by krnishant027 | 18 Sep, 2020, 01:37: PM
ANSWERED BY EXPERTCBSE 10 - Maths
Asked by technicalboy43 | 17 Mar, 2020, 08:47: AM
ANSWERED BY EXPERT
