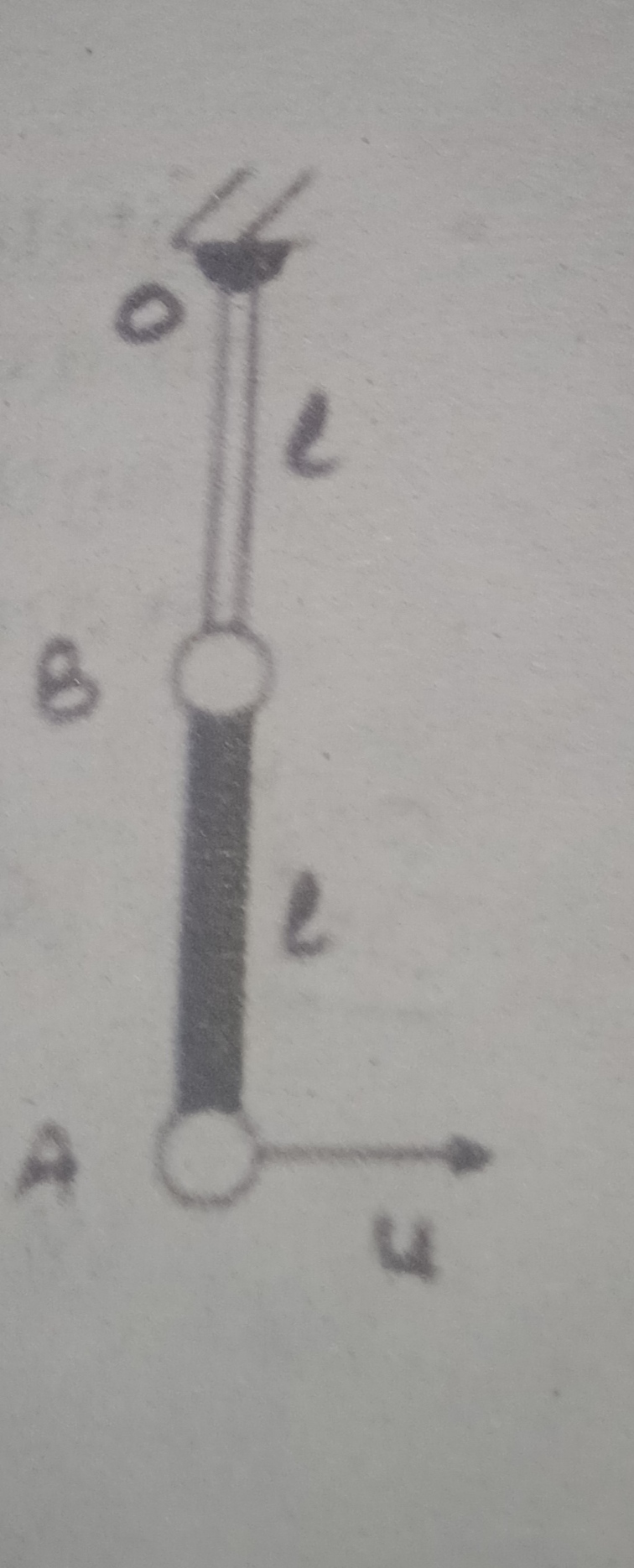CBSE Class 12-science Answered
A uniform rod of length L lies on a smooth horizontal table. A particle moving on the table strikes the rod perpendicularly at an end and then stops. Find the distance travelled by the centre of the rod by the time it rotates by a right angle.
Asked by rushabhjain.avv | 04 Dec, 2019, 07:07: PM

Figure shows a small mass m moving with initial speed vo strikes the rod of mass M and length L at end .
Initial total linear momentum is due to movement of mass only. After collision, mass m comes to rest.
Let us assume centre of mass of rod moves with speed vc .
Hence By conservation of linear momentum, we have mvo = M vc
Hence we get, vc = (m/M) vo ......................(1)
Initial angular momentum just before collision, mvo (L/2)
Angular momentum of rod just after collision = I ω = (ML2 /12) ω
where I is moment of inertia and ω is angular speed.
When angular momentum is taken about centre of mass, by conservation of angular momentum,
we have, mvo (L/2) = (ML2 /12) ω
hence angular velocity ω = 6(m/M) (vo / L ) .......................(2)
When angular momentum is taken about point of collision, by conservation of angular momentum,
we have, Iω - Mvc (L/2) = 0 .......................(3)
using moment of inertia, we write, (ML2/12) ω = M vc (L/2) i.e, ωL = 6 vc ..........(4)
By conservation of kinetic energy,
(1/2) m vo2 = (1/2) I ω2 + (1/2)M vc2
Let us substitute for ω and vc using eqn.(1) and (2) in the above eqn., then we have
(1/2) m vo2 = (1/2) ( ML2 / 12 ) [ (6mvo )/(ML) ]2 + (1/2)M [ (m/M) v0 ]2
By simplifying above eqn., we get, m/M = 1/4 ....................(5)
From eqn.(1), we get , vc = ( vo / 4 ) .....................(6)
if the rod has turned π/2 , time t for this rotation = ( π/2 ) / ω ...............(7)
time duration t for π/2 rotation , t = ( π/2 ) / ( 6vc / L) = ( π/2 ) / [ 3 vo / ( 2L) ] = (πL) / ( 3vo )
Distance moved by centre of mass = vc × t = ( vo / 4 ) × [ (πL) / ( 3vo ) ] = (π/12)L
Answered by Thiyagarajan K | 04 Dec, 2019, 10:07: PM
Concept Videos
CBSE 12-science - Physics
Asked by panneer1766 | 24 Apr, 2024, 01:52: PM
CBSE 12-science - Physics
Asked by artabandhusahu85 | 24 Apr, 2024, 12:07: PM
CBSE 12-science - Physics
Asked by niharvijayvargiya5 | 23 Apr, 2024, 06:40: PM
CBSE 12-science - Physics
Asked by kulhariabhijeet | 21 Apr, 2024, 02:39: PM
CBSE 12-science - Physics
Asked by mohapatraswetalina88 | 21 Apr, 2024, 12:18: PM
CBSE 12-science - Physics
Asked by aishaisha091098 | 19 Apr, 2024, 04:54: PM
CBSE 12-science - Physics
Asked by dasrituparna1999 | 13 Apr, 2024, 06:56: AM
CBSE 12-science - Physics
Asked by dasrituparna1999 | 12 Apr, 2024, 09:26: PM
CBSE 12-science - Physics
Asked by mishrigupta19319 | 08 Apr, 2024, 06:28: PM