Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

ICSE Class 10 Answered

a metal container is in the form of cylinder is surmounted by hemisphere of the same radius .the internal height of the cylinder is 7m and internal radius of the cylinder is 3.5m .calculate the total surface area of the internal surface excluding the base and find the internal volume of the container in m3
Asked by eswarandevi375 | 19 Nov, 2023, 03:06: PM
answered-by-expert Expert Answer
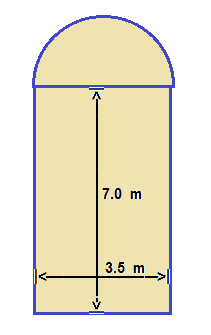
Figure shows the container which is a cylinder surmounted by a hemisphere .
 
Let d = 3.5 m be the internal diameter of cylinder and h = 7.0 m be the height of cylinder .
 
Inner surface area S1 of cylindrical part of container = ( π d h ) + (π/4) d2 = π d [  h + ( d2 / 4 ) ]
 
( First term of above expression for curved surface area and second term for bottom surface area )
 
begin mathsize 14px style S subscript 1 space equals space pi cross times space 3.5 space cross times open square brackets 7 space plus space fraction numerator 3.5 cross times 3.5 over denominator 4 end fraction close square brackets space space equals space 110.6 space m squared end style
Inner surface area s2 of hemispherical part of container = 2π (d/2)2  = π (d2 / 2 )
 
begin mathsize 14px style S subscript 2 space equals space pi space cross times fraction numerator 3.5 cross times 3.5 over denominator 2 end fraction space m squared space equals space 19.2 space m squared end style
Total inner surface area = S1 + S2 = (110.6 + 19.2 ) m2 = 129.8 m2
 
-----------------------------------------------------
 
Inner volume V1 of cylindrical part of container = (π/4) d2 h
 
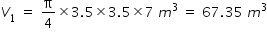
begin mathsize 14px style V subscript 1 space equals space straight pi over 4 cross times 3.5 cross times 3.5 cross times 7 space m cubed space equals space 67.35 space m cubed end style
 
Inner volume V2 of hemispherical part of container = (2/3)π (d/2)3 = (1/12) π d3
 
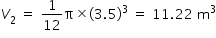
begin mathsize 14px style V subscript 2 space equals space 1 over 12 straight pi cross times left parenthesis 3.5 right parenthesis cubed space equals space 11.22 space straight m cubed end style
Total Inner volume = V1 + V2 = 78.57 m3

 
Answered by Thiyagarajan K | 19 Nov, 2023, 04:30: PM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×