CBSE Class 12-science Answered

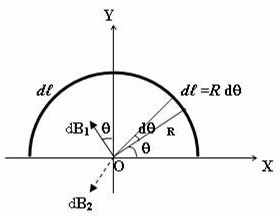
The question setter requires you to calculate the magnetic flux density at points on the axis (of the semicircular ring shaped cross section of the infinitely long wire). In the adjoining figure we have shown the cross section (of the given wire) lying in the XY plane. The length of the wire is along the Z-axis and the current in the wire is supposed to flow along the negative Z-direction. The broad infinitely long wire can be imagined to be made of a large number of infinitely long straight wire strips, each of small width d?.

With reference to the figure, we have d? = Rd?.

The magnetic flux density due to the above strip is shown as dB₁ in the figure. It has an X-component dB₁ sin? and a Y-component dB₁cos?. When we consider a similar strip of the same with d? located symmetrically with respect to the Y-axis, we obtain a contribution dB₂ to the flux density. The flux density dB₂ has the same magnitude as dB₁. It has X-component dB₂ sin? and Y-component dB₂cos?. The X-components of dB₁ and dB₁ are of the same magnitude and direction and they add up. But the Y-components of dB₁ and dB₁ are in opposite directions and have thesame magnitude. Therefore they get canceled. The entire conductor therefore produces a resultantmagnetic field along the negative X-direction.

The wire strip of width d? cn be imagined to be an ordinary thin straight infinitely long wire carrying current Id?/?R since the total current I flows through the semicircular cross section of perimeter ?R. Putting dB₁ = dB₂ = dB we have

dB = ?₀ (Id?/?R)/2?R = ?₀ (IRd?/?R)/2?R = ?₀Id?/2?²R

The X-component of the above field is (?₀I/2?²R) sin? d?

The field due to the entire conductor is B = ₀?^? [(?₀I/2?²R) sin?]d?

Or, B = ?₀I/?²R since ₀?^? sin? d? = 2