A circular loop of radius a is placed in a diverging magnetic field B such that the angle between the normal to the plane of the loop and field anywhere on the loop is θ. Also, the magnetic field present is such that the lines cut the loop at 900. Derive an expression for the net force exerted by the field on the loop when a current i is made to flow through the loop.
Asked by Topperlearning User
| 28th Apr, 2015,
02:05: PM
Expert Answer:
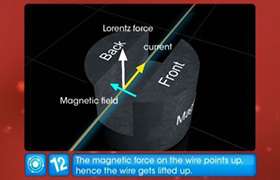
Let us consider an infinitesimal segment of the loop of length ds.
The magnetic field is perpendicular to all the segments of the loop.
Force on this segment, dF = iBds
Horizontal component of the force, dFH = (iB cosθ)ds
This component of the force points away from the loop.
Vertical component of the force, dFv = (iB sinθ)ds
This component of the force points upward from the plane of the loop.
When we sum each of these components for all segments of the loop, the sum of horizontal component of the force vanishes. This happens because the horizontal force acting on the diametrically -opposite segments of the loop cancel each other out. As a result, only the vertical component of the force contributes to the net force on the loop.
The vertical component, which points upward, is
Fv = iB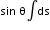 
= (2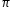
a)iB sinθ (Since i,B, θ are constants)
Answered by
| 28th Apr, 2015,
04:05: PM
Concept Videos
- A magnetized needle of magnetic moment 4.6 × 10-2 JT-1 is placed at 30o with the direction of a uniform magnetic field of strength 4 × 10-2 T. a. What is the torque acting on it ?b. How much work is required for it to make a 120o angle with the magnetic field?
- Derive an expression for the torque acting on a loop of N turns, area A, carrying current i, when held in a uniform magnetic field.
- A circular coil of 200 turns, radius 5 cm carries a current of 2.5 A. It is suspended vertically in a uniform horizontal magnetic field of 0.25 T, with the plane of the coil making an angle of 60o with the field lines. Calculate the magnitude of the torque that must be applied on it to prevent it from turning.
- State the underlying principle of working of a moving coil galvanometer. Write two reasons why a galvanometer cannot be used as such to measure current in a given circuit. Name any two factors on which the current sensitivity of a galvanometer depends.
- A circular coil of 200 turns and radius 10 cm is placed in a uniform magnetic field of 0.5 T, normal to the plane of the coil. If the current in the coil is 3.0 A, calculate the (a) Total torque on the coil (b) Total force on the coil (c) Average force on each electron in the coil due to the magnetic field Assume the area of cross-section of the wire to be 10-5m2 and the free electron density is 1029/m3.
- With the help of a neat and labelled diagram, explain the underlying principle and working of a moving coil galvanometer.
- What is meant by current sensitivity of a moving coil galvanometer? On what factors does it depend?In an exercise to increase the current sensitivity of a galvanometer by 25%, its resistance is also increased 1.5 time. How will the voltage sensitivity of the meter be affected?
- How the magnetic moment of an electron will change if we double the frequency of its revolution?
- A current loop is considered as a magnetic dipole. Explain.
Kindly Sign up for a personalised experience
- Ask Study Doubts
- Sample Papers
- Past Year Papers
- Textbook Solutions
Sign Up
Verify mobile number
Enter the OTP sent to your number
Change