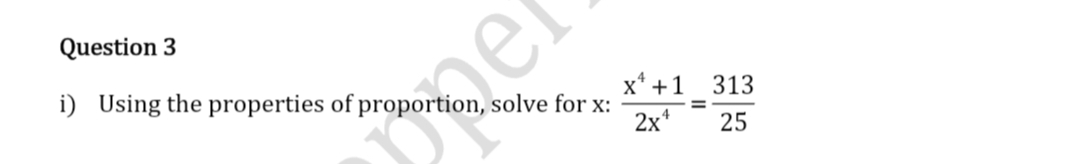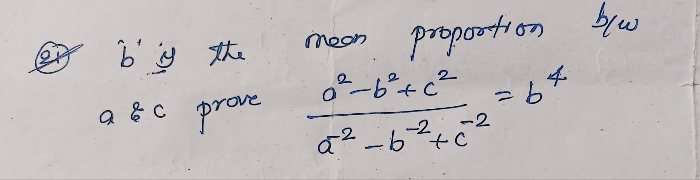ICSE Class 10 Answered
a, b, c are in continued proportion , prove that a\c = 2a2−5ab+7b2\2b2−5bc+ 7c2
Asked by tafeelsayyed786 | 19 Sep, 2020, 01:56: PM
Given: a, b and c are in continued proportion

Answered by Renu Varma | 22 Sep, 2020, 02:11: PM
Concept Videos
ICSE 10 - Maths
Asked by vrj.parmar369 | 07 Mar, 2024, 11:27: AM
ICSE 10 - Maths
Asked by ng028277 | 27 Jan, 2024, 07:36: PM
ICSE 10 - Maths
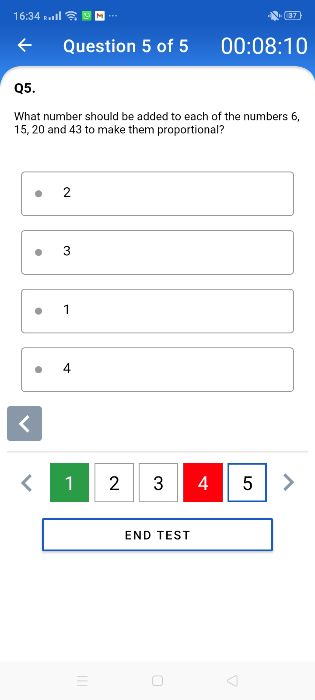
Asked by kalayani822 | 09 Oct, 2023, 08:25: AM
ICSE 10 - Maths
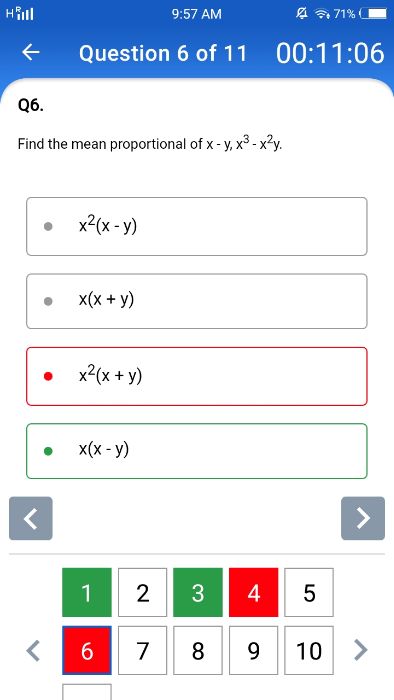
Asked by nehalmukhia53 | 21 Jun, 2022, 07:46: PM
ICSE 10 - Maths
Asked by shaikazheruddin245 | 16 Feb, 2022, 02:50: PM
ICSE 10 - Maths
Asked by harendrapratapsingh8858 | 18 Nov, 2021, 04:34: PM
ICSE 10 - Maths
Asked by anumatiravi14 | 30 Sep, 2021, 10:09: AM
ICSE 10 - Maths
Asked by brijt66 | 05 Aug, 2021, 06:28: AM
ICSE 10 - Maths
Asked by umeshkumargouda1 | 16 Jun, 2021, 07:15: PM