CBSE Class 11-science Answered
7th sum
Asked by lovemaan5500 | 02 Feb, 2019, 08:26: PM
Expert Answer
Let a be the first term and d be the common difference of an AP.
tp = a + (p - 1)d
tq = a + (q - 1)d
tr = a + (r - 1)d
According to the question terms are in GP
[a + (q - 1)d]2 = [a + (p - 1)d][a + (r - 1)d]
simplifying this we get
a =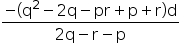 
and r =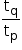 
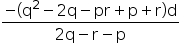and r =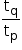 Solving r =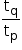
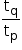
we get r =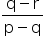 
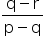
Answered by Sneha shidid | 04 Feb, 2019, 01:04: PM
CBSE 11-science - Maths
Asked by sanjuktamukherjee165 | 24 Oct, 2021, 11:04: AM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by Vibhorjarora798 | 21 Aug, 2021, 05:43: PM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by hirugadeshravani | 26 Dec, 2020, 07:37: AM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by pavanindr | 09 Feb, 2020, 04:56: PM
ANSWERED BY EXPERT
CBSE 11-science - Maths
Asked by lovemaan5500 | 28 Jan, 2019, 06:29: AM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by shaikh.farid25 | 05 Nov, 2018, 07:03: PM
ANSWERED BY EXPERT
