Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 12-science Answered

55Cs124(Z=55,A=124) has a half life of 30.8s. (a) If we have 7.8 microgram initially, how many nuclei are presents? How many are present 2 min later? (b) What is the activity at this time? (c) After how much time will the activity drop to less than about 1 per second?
Asked by arjunsah797 | 16 May, 2022, 02:17: PM
Expert Answer
Part (a)
 
Number of atoms in w gram = ( N / A ) × w
 
where N = 6.022 × 1023 is Avagadro number and A is atomic weight
 
Number of atoms in  7.8 microgram = ( 6.022 × 1023  / 124 ) × 7.8 × 10-6 = 3.788 × 1016
 
Number of nuclei at present, No = 3.788 × 1016
 
Number N of nuclei after 2 min is determined from radioactivity equation
 
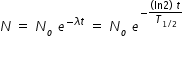
begin mathsize 14px style N space equals space N subscript o space e to the power of negative lambda t end exponent space equals space N subscript o space e to the power of negative fraction numerator left parenthesis ln 2 right parenthesis space t over denominator T subscript 1 divided by 2 end subscript end fraction end exponent end style
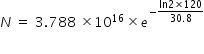
begin mathsize 14px style N space equals space 3.788 space cross times 10 to the power of 16 to the power of space end exponent cross times e to the power of negative fraction numerator ln 2 cross times 120 over denominator 30.8 end fraction end exponent end style
N = 2.544 × 1015
 -----------------------------------------------
Part (b)
 
Activity after 2 mins is calculated from the following relation
 
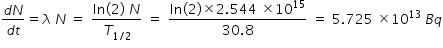
begin mathsize 14px style fraction numerator d N over denominator d t end fraction equals lambda space N space equals space fraction numerator ln left parenthesis 2 right parenthesis space N over denominator T subscript 1 divided by 2 end subscript end fraction space equals space fraction numerator ln left parenthesis 2 right parenthesis cross times 2.544 space cross times 10 to the power of 15 over denominator 30.8 end fraction space equals space 5.725 space cross times 10 to the power of 13 space B q end style
------------------------------------------------
Part (c)
 
Radioactivity is given as ( dN/dt ) = λ N
 
If (dN/dt ) = 1 Bq ,  then N = 1/λ  = T1/2 / ln(2) ≈ 44

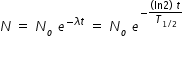
begin mathsize 14px style N space equals space N subscript o space e to the power of negative lambda t end exponent space equals space N subscript o space e to the power of negative fraction numerator left parenthesis ln 2 right parenthesis space t over denominator T subscript 1 divided by 2 end subscript end fraction end exponent end style
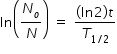
begin mathsize 14px style ln open parentheses N subscript o over N close parentheses space equals space fraction numerator left parenthesis ln 2 right parenthesis t over denominator T subscript 1 divided by 2 end subscript end fraction end style
t = [ ln( No / N ) × T1/2 ] / (ln2)
 
after substituting values No = 2.544 × 1015 , N = 44 , T1/2 = 30.8 s , we get
 
t = 1408 s = 23 min 28 s
Answered by Thiyagarajan K | 16 May, 2022, 03:16: PM

Concept Videos

Multiple Choice Questions Practice Test Subjective Questions Webinar Subjective Questions Pre Board Assessment
Answered Unanswered My Questions My Answers
CBSE 12-science - Physics
55Cs124(Z=55,A=124) has a half life of 30.8s. (a) If we have 7.8 microgram initially, how many nuclei are presents? How many are present 2 min later? (b) What is the activity at this time? (c) After how much time will the activity drop to less than about 1 per second?
Asked by arjunsah797 | 16 May, 2022, 02:17: PM
ANSWERED BY EXPERT
CBSE 12-science - Physics
how are we supposed to solve this question
Asked by merinlijo_20002 | 17 Jun, 2020, 10:05: AM
ANSWERED BY EXPERT
CBSE 12-science - Physics
Carbon-14(C14) decays at a constant rate in such a way that it reduces to 50% in 5568 years. Find the age of an old wooden piece in which the carbon is only 25% of the original.
Asked by rajubarman | 01 Dec, 2019, 10:03: AM
ANSWERED BY EXPERT
CBSE 12-science - Physics
Radioactive nuclei 
Asked by alanpeter9611 | 23 Feb, 2019, 07:47: PM
ANSWERED BY EXPERT
CBSE 12-science - Physics
Radioactive elements 
Asked by alanpeter9611 | 22 Feb, 2019, 11:24: PM
ANSWERED BY EXPERT
CBSE 12-science - Physics
Half-life period of a radioactive sample is 2 days. If the number of nuclei initially present isN subscript 0, find the number of nuclei present after 8 days?
Asked by sd2021667 | 04 Dec, 2018, 04:46: PM
ANSWERED BY EXPERT
CBSE 12-science - Physics
figure for 13.6 in chapter nuclei  
Asked by silladech | 16 Nov, 2018, 11:14: AM
ANSWERED BY EXPERT
CBSE 12-science - Physics
The half life period of a radioactive substance is 30 days. What is the time for ¾ th of its original mass to disintegrate?
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
ANSWERED BY EXPERT
CBSE 12-science - Physics
How many α and β-partiles are emitted 90Th232 changes to 82Pb208?
Asked by Topperlearning User | 09 Jul, 2014, 04:06: PM
ANSWERED BY EXPERT
CBSE 12-science - Physics
  Complete the following nuclear reactions (a) 4Be9 + 1H1 →3Li6 + ................ (b) 5B10 + Syntax error from line 1 column 49 to line 1 column 73. Unexpected '<mstyle '. → Syntax error from line 1 column 49 to line 1 column 73. Unexpected '<mstyle '. + ..............  
Asked by Topperlearning User | 09 Jul, 2014, 04:15: PM
ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt