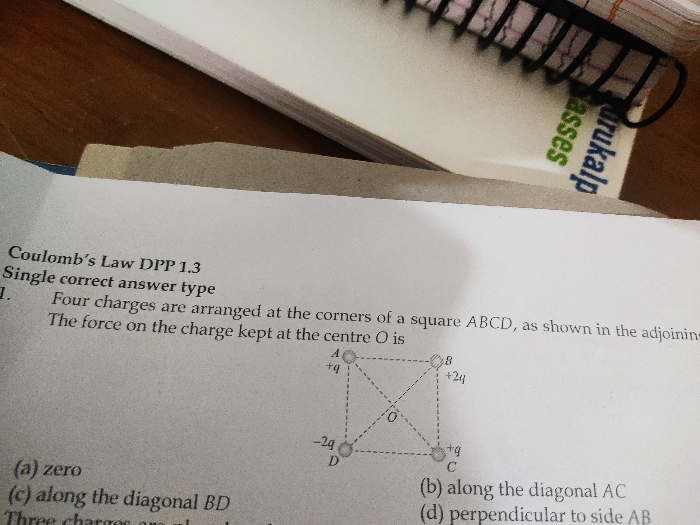Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

JEE Class main Answered

3point charge q, -2q, and 4q are kept at 3 vertices of a equilateral triangle find net force on each of them
Asked by marshelojigas | 27 Jun, 2022, 06:03: AM
answered-by-expert Expert Answer
 
 
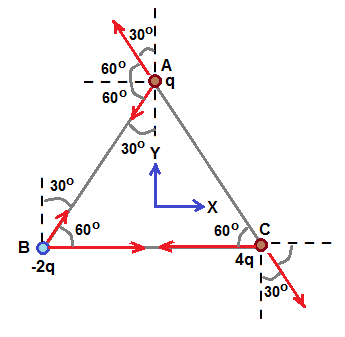
Figure shows the charge configuration on an equilateral triangle of side a as given in the question .
 
Type of force between charges,  whetherforce is  attractive or repulsive,  is decided depends on sign of charges .
 
Force FA on a charge q at vertex A is determined as follows .

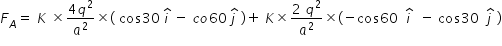
begin mathsize 14px style F subscript A equals space K space cross times fraction numerator 4 q squared over denominator a squared end fraction cross times left parenthesis space cos 30 space i with hat on top space minus space c o 60 space j with hat on top space right parenthesis plus space K cross times fraction numerator 2 space q squared over denominator a squared end fraction cross times left parenthesis negative cos 60 space space i with hat on top space space minus space cos 30 space space j with hat on top space right parenthesis end style
where K = 1/ ( 4πεo ) is Coulomb's constant  , a is side of triangle ,
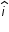begin mathsize 14px style i with hat on top end style is unit vector along +x axis direction and begin mathsize 14px style j with hat on top space end style is +y axis direction
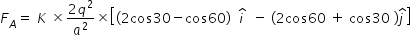
begin mathsize 14px style F subscript A equals space K space cross times fraction numerator 2 q squared over denominator a squared end fraction cross times open square brackets left parenthesis 2 cos 30 minus cos 60 right parenthesis space space i with hat on top space space minus space left parenthesis 2 cos 60 space plus space cos 30 space right parenthesis j with hat on top close square brackets end style
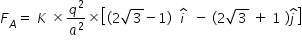
begin mathsize 14px style F subscript A equals space K space cross times q squared over a squared cross times open square brackets left parenthesis 2 square root of 3 minus 1 right parenthesis space space i with hat on top space space minus space left parenthesis 2 square root of 3 space plus space 1 space right parenthesis j with hat on top close square brackets end style
Magnitude of FA  is given as
 
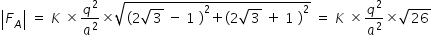
begin mathsize 14px style open vertical bar F subscript A close vertical bar space equals space K space cross times q squared over a squared cross times square root of left parenthesis 2 square root of 3 space minus space 1 space right parenthesis squared plus left parenthesis 2 square root of 3 space plus space 1 space right parenthesis squared end root space equals space K space cross times q squared over a squared cross times square root of 26 end style
-----------------------------

Force FB on a charge -2q at vertex B is determined as follows .

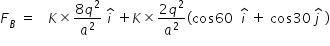
begin mathsize 14px style F subscript B space equals space space space K cross times fraction numerator 8 q squared over denominator a squared end fraction space i with hat on top space plus K cross times fraction numerator 2 q squared over denominator a squared end fraction left parenthesis cos 60 space space i with hat on top space plus space cos 30 space j with hat on top space right parenthesis end style
 
 
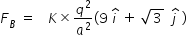
begin mathsize 14px style F subscript B space equals space space space K cross times q squared over a squared left parenthesis 9 space i with hat on top space plus space square root of 3 space space j with hat on top space right parenthesis end style
Magnitude of FB  is given as
 
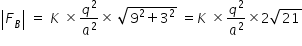
begin mathsize 14px style open vertical bar F subscript B close vertical bar space equals space K space cross times q squared over a squared cross times space square root of 9 squared plus 3 squared end root space equals K space cross times q squared over a squared cross times 2 square root of 21 end style
-----------------------------
Force FC on a charge 4q at vertex C is determined as follows .

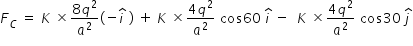
begin mathsize 14px style F subscript C space equals space K space cross times fraction numerator 8 q squared over denominator a squared end fraction left parenthesis negative i with hat on top space right parenthesis space plus space K space cross times fraction numerator 4 q squared over denominator a squared end fraction space cos 60 space i with hat on top space minus space space K space cross times fraction numerator 4 q squared over denominator a squared end fraction space cos 30 space j with hat on top end style
 
 
 
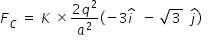
begin mathsize 14px style F subscript C space equals space K space cross times fraction numerator 2 q squared over denominator a squared end fraction left parenthesis negative 3 i with hat on top space space minus space square root of 3 space space j with hat on top right parenthesis space space space end style
Magnitude of FC is given as
 
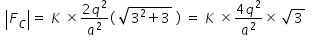
begin mathsize 14px style space open vertical bar F subscript C close vertical bar equals space K space cross times fraction numerator 2 q squared over denominator a squared end fraction left parenthesis space square root of 3 squared plus 3 end root space right parenthesis space equals space K space cross times fraction numerator 4 q squared over denominator a squared end fraction cross times space square root of 3 space space space end style
Answered by Thiyagarajan K | 27 Jun, 2022, 08:42: AM
Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
JEE main - Physics
what is dipole
Asked by manishkanna555 | 07 Jul, 2024, 10:25: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
Three Charges -q,+q and -q are placed at the corner of an equilateral triangle of side a . the resultant electric force on a charge +q placed at the centroid O of the triangle is
Asked by chandana9827 | 13 Jun, 2024, 20:28: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
physics
question image
Asked by arnendubiswas5 | 28 May, 2024, 09:27: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
doubt
question image
Asked by pkp7734825 | 04 May, 2024, 22:30: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
Three equal charges, 2?0 × 10 ? 6 C each, are held fixed at the three corners of an equilateral triangle of side 5 cm. Find the Coulomb force experienced by one of the charges due to the rest two.
question image
Asked by ratnadeep.dmr003 | 21 Apr, 2024, 23:06: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
solution of 12th question
question image
Asked by medhamahesh007 | 02 Apr, 2024, 11:11: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
four charges are arranged at corners of square abcd as in figur the force on charge kept at centre o is
question image
Asked by chhayasharma9494 | 31 Mar, 2024, 12:47: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
two small conducting spheres each of mass 9×10??kg qre suspended from the same point by non conducting strings of length 100cm. they are given equal and similar charges until the strings are rqually inclined at 45° each to the vertcal. The charge on each sphere is
Asked by archithateja3 | 30 Mar, 2024, 22:23: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
solve
question image
Asked by rishabhtiwari2027 | 21 Mar, 2024, 21:44: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
an electric dipole placed with its access in the direction of electric field experience
Asked by mfkatagi099 | 20 Mar, 2024, 21:35: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt