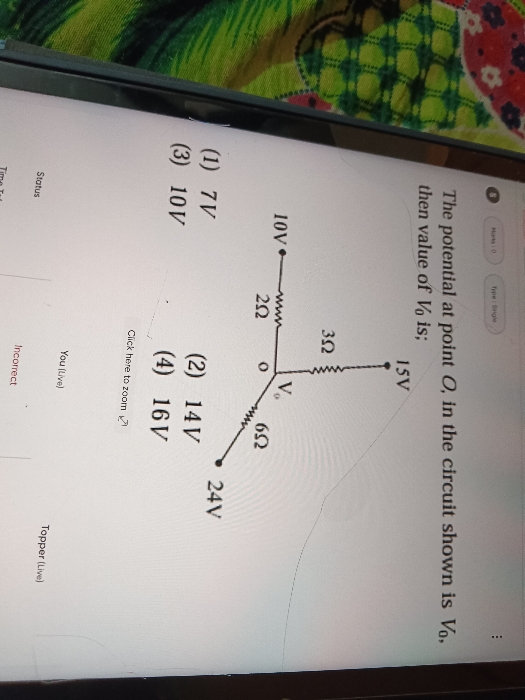
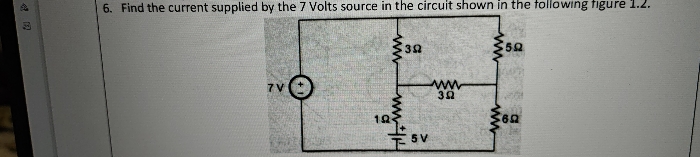
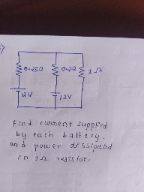
CBSE Class 12-science Answered

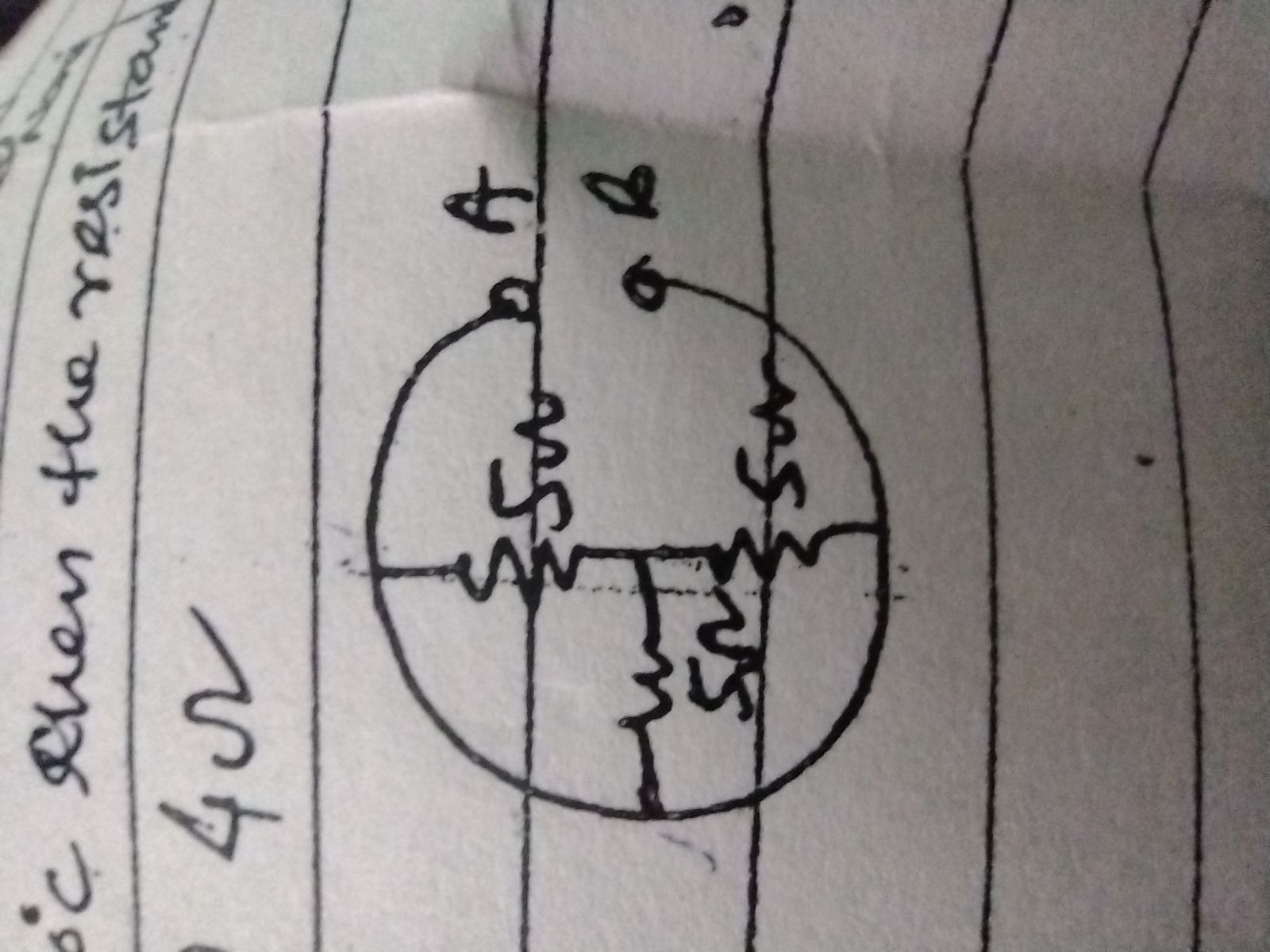
16. A wire of resistance 3? is cut into three pieces and then each piece is stretched to three times of length. These pieces are connected in parallel and connected across a battery of emf 3 V. Find the current through each resistance.

Asked by Sudheer Nair | 28 Feb, 2012, 02:12: PM

Expert Answer

Wire is cut inro three pieces so each wire will have resistance = 1 ohm

We use:-
R = (rho x L) /A
Where: R = resistance in (Ohms) ; rho the resistivity of copper; L = the length of the wire (m) and A is the cross sectional area of the wire (m^2).

The resistance of original length we can represent as:-
R1 = (rho x L1)/A1
and the final length as:-
R2 = (rho x L2)/A2

In these two one thing is constant: rho. So we re-arrange both equations for rho and then equate them. This gives:-

rho = (R1 x A1)/L1 and
rho = (R2 x A2)/L2

Now, we equate them to give:-
(R1 x A1)/L1=(R2 x A2)/L2

Now, when the wire is stretched the new length changes to three times it's original, so we can write:-
L2 =3 x L1

But, what is the change in the area?
To calculate this we need to use something else that does not change, this time the volume.

The original wire length can be thought of as a very long thin cyclinder with a volume =pi x r1^2 x L1
which is then drawn out by the extrusion process to pi x r2^2 x L2. Both volumes will be identical so This means that we can write:-

V1 = V2
pi x r1^2 x L1 = pi x r2^2 x L2
But since L2 = 3 x L1 then we have:-
pi x r1^2 x L1 = pi x r2^2 x 3 x L1

re-arranging we get: r1^2/r2^2 = (pi x 3 x L1)/(pi x L1)
r1^2/r2^2 = 3
Therefore, when the wire is stretched to three times it original length the area, A2 is reduced to one third ( and the radius BTW is reduced to x 1/root (3).
This means that the new radius r2^2 is given by
r2^2 =(r1^2) /3
and we can use this to calculate the new area, A2.

We have already found that:-
(R1 x A1)/L1=(R2 x A2)/L2 so,
we now say
(R1 x pi x r1^2)/L1 =(R2 x pi x ((r1^2)/3))/(3 x L1)
(R1 x pi x r1^2)/L1 = (R2 x pi x r1^2)/(3 x 3 x L1)

R1/R2 = (pi x r1^2 x L1)/(9 x pi x r1^2 x L1)

R1/R2 =1/9

Hence R2/R1= 9

R2 = 9 x R1

R2 = 9 ohms

Now the 3 wires each of 9 ohms are connected in parallel so final resistance = 3 ohms

Current = 3/3 = 1 Ampere

Answered by | 01 Mar, 2012, 10:29: AM