Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 11-science Answered

1. Write the equations of motion which govern the motion of centre of mass  2. Derive an expression for torque in cartesian coordinates
Asked by fishtailfever | 03 Nov, 2019, 11:01: PM
answered-by-expert Expert Answer
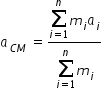
begin mathsize 14px style a subscript C M end subscript space equals fraction numerator begin display style sum from i equals 1 to n of end style m subscript i a subscript i over denominator begin display style sum from i equals 1 to n of end style m subscript i end fraction end style
where aCM is acceleration of centre of mass, ai is acceleration of individual objects that hass mass mi
-----------------------------------------------------------
 
Torque τ of force F acting on a body is,  τ = r × F
 
where r is position vector of point of application of force with respect to reference point.
 
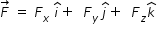Let begin mathsize 14px style r with rightwards arrow on top space equals space x space i with hat on top plus space y space j with hat on top space plus space z k with hat on top space end style and begin mathsize 14px style F with rightwards arrow on top space equals space F subscript x space i with hat on top plus space space F subscript y space j with hat on top plus space space F subscript z k with hat on top end style.
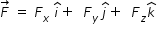Then the torque τ is given by
 
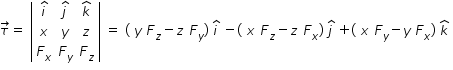
begin mathsize 14px style tau with rightwards arrow on top equals space open vertical bar table row cell i with hat on top end cell cell j with hat on top end cell cell k with hat on top end cell row x y z row cell F subscript x end cell cell F subscript y end cell cell F subscript z end cell end table close vertical bar space equals space left parenthesis space y space F subscript z minus z space F subscript y right parenthesis space i with hat on top space minus left parenthesis space x space F subscript z minus z space F subscript x right parenthesis space j with hat on top space plus left parenthesis space x space F subscript y minus y space F subscript x right parenthesis space k with hat on top space end style
Answered by Thiyagarajan K | 04 Nov, 2019, 08:04: AM
Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 11-science - Physics
the question
question image
Asked by rajeshabirami27 | 07 May, 2024, 04:31: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
A train starts from a station with a constant acceleration of 4 m/s2. Two seconds later another train passes the same station on the same line and in the same direction with a constant velocity. Find the velocity if the collision is first averted
Asked by yatin1043 | 06 May, 2024, 02:47: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
1
question image
Asked by pc2091054 | 05 May, 2024, 10:43: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
answer me
question image
Asked by sheikhsaadat24 | 17 Apr, 2024, 09:41: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
.A SHM is expressed by the equation x = A cos (ωt + φ) and the phase angle φ =0. Draw graphs to show variation of displacement, velocity and acceleration for one complete curve in SHM.
Asked by sy123946 | 07 Apr, 2024, 04:23: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
the dimension of stopping potential vo in photoelectric effect in units of plank's constant 'h',speed of light 'c' and gravitational constant 'G' and ampereA
Asked by derhebha955 | 03 Apr, 2024, 09:03: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
In this que while solving it we take D F of alpha =D.F of beta.Why is it so?
question image
Asked by sumedhasingh238 | 29 Mar, 2024, 05:15: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
In physics if 2 quantities are dimensionless then their dimensional formula are equal?
Asked by sumedhasingh238 | 28 Mar, 2024, 11:10: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
7. State the relation between maximum range and maximum height of the projectile if the angle of projection is 45 deg
Asked by roshnibudhrani88 | 23 Mar, 2024, 05:52: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
The second overtone of a pipe closed at one end has the same frequency as the third overtone of a pipe open at both ends. Compare the length of the pipes
Asked by emad.amd | 21 Mar, 2024, 12:00: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×