CBSE Class 11-science Answered
1> 1\2.5+1\5.8+......+1\(3n-1)(3n+2)=n\(6n+4)
Asked by visakha | 30 Nov, 2013, 06:22: PM
Let S(n) : 1/2.5+1/5.8+1/8.11 +.... + 1/(3n-1)(3n+2) = n/(6n+4)
Let us prove S(n) for n=1.
LHS =1/2.5 =1/10; RHS = 1/6+4=1/10
So it is true for n=1.
Assume that S(n) is true for some n=k.
1/2.5+1/5.8+1/8.11 +.... + 1/(3k-1)(3k+2) = k/(6k+4)
Now, we will prove S(n) for n=k+1
LHS = 1/2.5+1/5.8+1/8.11 +.... + 1/(3(k+1)-1)(3(k+1)+2)
=k/(6k+4) + 1/(3k+2)(3k+5)
=k/2(3k+2) + 1/(3k+2)(3k+5)
=[k(3k+5)+2]/[2((3k+2)(3k+5)]
=[3k^2+5k+2]/[2((3k+2)(3k+5)]
=[(3k+2)(k+1)]/[2((3k+2)(3k+5)]
=(k+1)/2(3k+5)
=(k+1)/(6k+10)
= (k+1)/[6(k+1)+4]
=RHS
So it is true for n=k+1.
Thus, by the principal of mathematical induction we can say that S(n) is true for all natural numbers n.
Answered by | 01 Dec, 2013, 01:15: AM
Concept Videos
CBSE 11-science - Maths
Asked by keeruzzzzz | 11 Mar, 2020, 07:35: PM
CBSE 11-science - Maths
Asked by syedaliasad649 | 01 Oct, 2019, 07:07: PM
CBSE 11-science - Maths
Asked by lovemaan5500 | 02 Feb, 2019, 08:24: PM
CBSE 11-science - Maths
Asked by Topperlearning User | 14 May, 2014, 03:21: PM
CBSE 11-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 11-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 11-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 11-science - Maths
Asked by Topperlearning User | 07 Aug, 2014, 08:49: AM
CBSE 11-science - Maths
Asked by Topperlearning User | 15 May, 2014, 10:48: AM
CBSE 11-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM







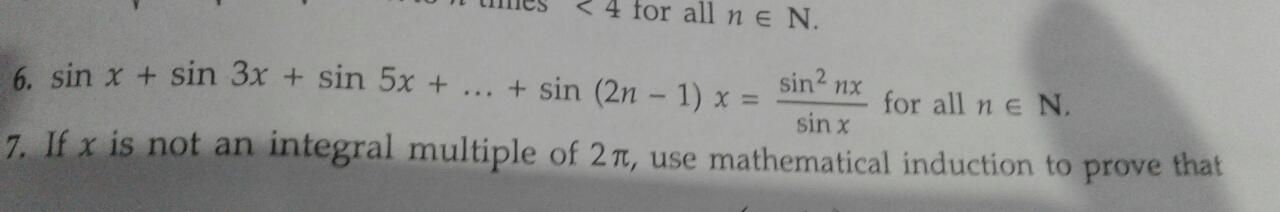
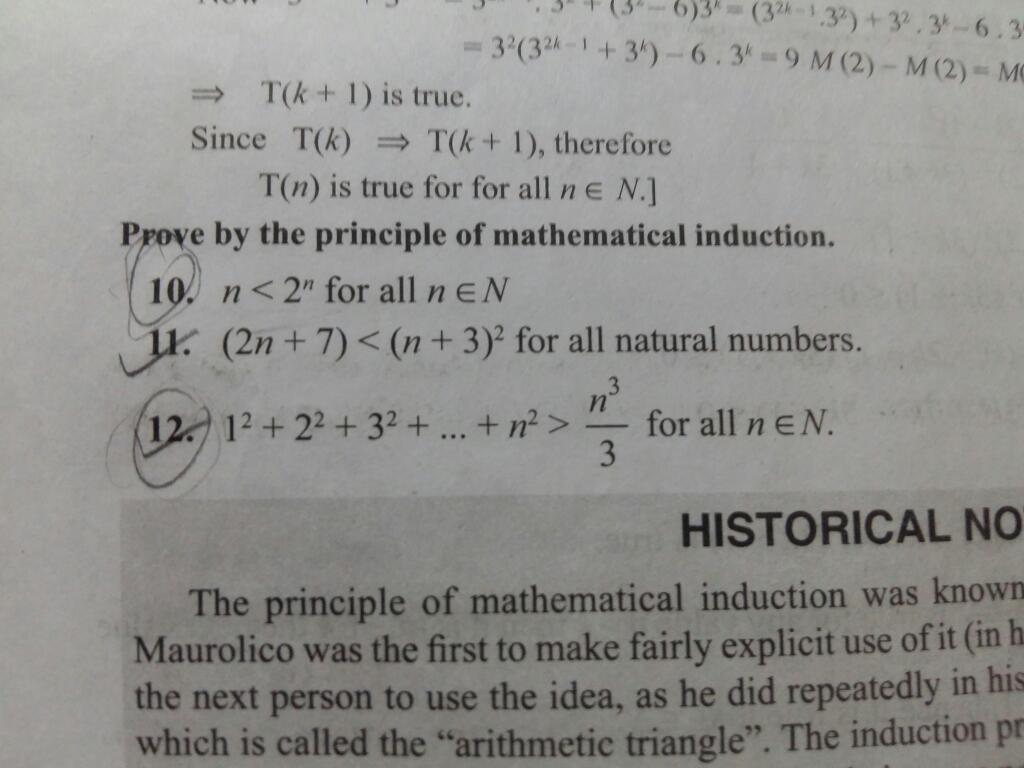
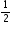 n(3n-1)
n(3n-1)