Class 9 FRANK Solutions Maths Chapter 19: Quadrilaterals
If you are given the measure of one angle of a parallelogram, can you find the measure of the remaining angles? You can by referring to our Frank Solutions for ICSE Class 9 Mathematics Chapter 19 Quadrilaterals during revision. Further, you can practise Maths questions and answers on how to prove that the given figure is a parallelogram or a rectangle.
The Frank textbook solutions at the TopperLearning portal even includes problems on providing proofs to show that the given quadrilateral is a rhombus. If you are looking for more such ICSE Class 9 Maths chapter solutions, check the Selina solutions and solved sample question papers.
Quadrilaterals Exercise Ex. 19.1
Solution 1(a)

Solution 1(b)

Solution 1(c)

Solution 1(d)

Solution 1(e)

Solution 2
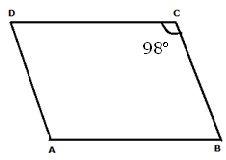

Solution 3

Solution 4

Solution 5

Solution 6

Solution 7

Solution 8
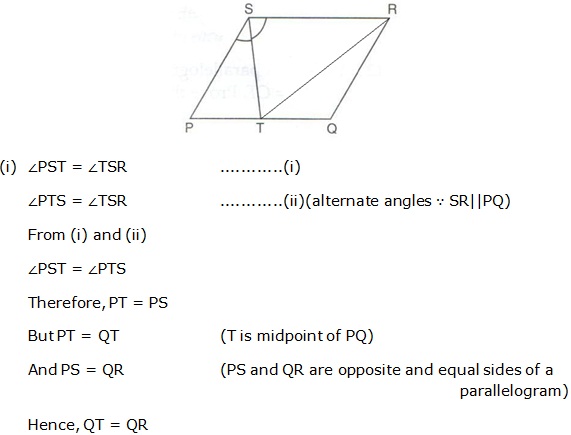

Solution 9

Solution 10

Solution 11

Solution 12

Solution 13
Construction: Join PR.


Solution 14
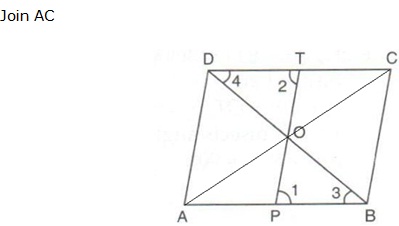

Solution 15

Quadrilaterals Exercise Ex. 19.2
Solution 1


Solution 2
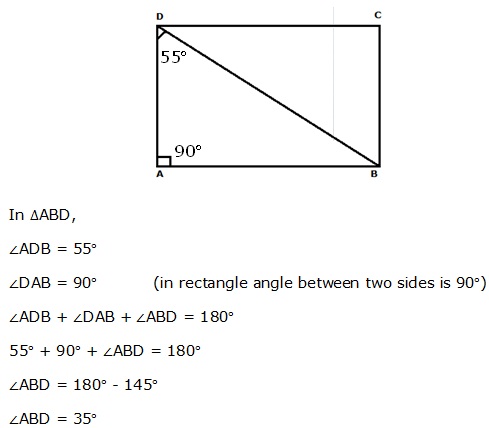
Solution 3
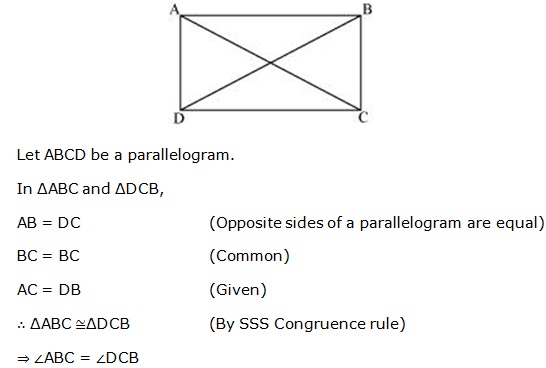

Solution 4




Solution 5
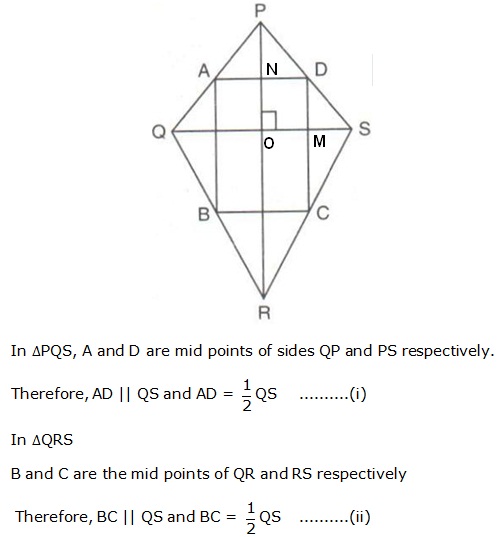

Solution 6
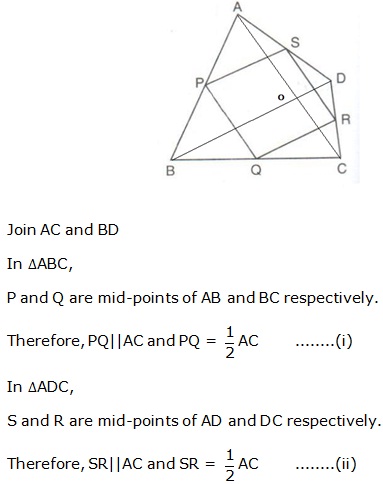

Solution 7


Solution 8


Solution 9
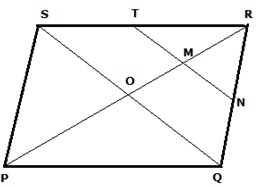

Solution 10

Solution 11
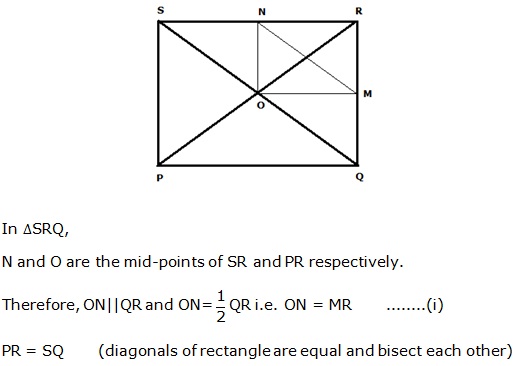

Solution 13(a)
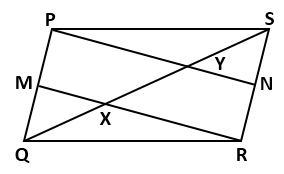

Solution 13(b)


Solution 13(c)
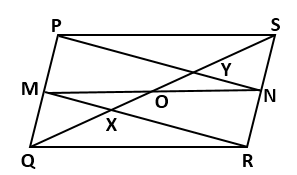

Solution 12
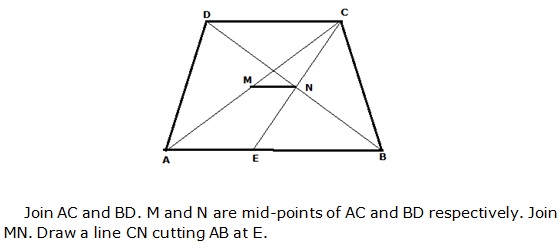

Solution 14


Solution 15(a)
Construction:
Join BS and AQ.
Join diagonal QS.
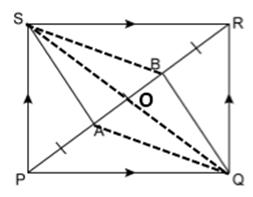

Solution 15(b)
Construction:
Join BS and AQ.
Join diagonal QS.
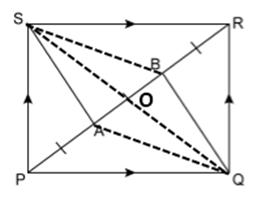

Solution 16(a)
Construction:
Draw SM ⊥ PQ and RN ⊥ PQ
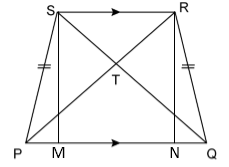

Solution 17
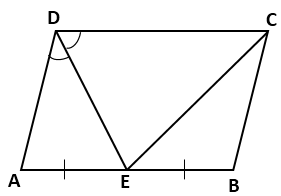

Solution 18
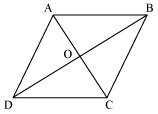
Let ABCD be a quadrilateral, whose diagonals AC and BD bisect each other at right angle.
i.e. OA = OC, OB = OD
And, ∠AOB = ∠BOC = ∠COD = ∠AOD = 90°
To prove ABCD a rhombus, we need to prove ABCD is a parallelogram and all sides of ABCD are equal.
Now, in ΔAOD and DCOD
OA = OC (Diagonal bisects each other)
∠AOD = ∠COD (Each 90°)
OD = OD (common)
∴ΔAOD ≅ΔCOD (By SAS congruence rule)
∴ AD = CD ….(i)
Similarly, we can prove that
AD = AB and CD = BC ….(ii)
From equations (i) and (ii), we can say that
AB = BC = CD = AD
Since opposite sides of quadrilateral ABCD are equal, so, we can say that ABCD is a parallelogram.
Since all sides of a parallelogram ABCD are equal, so, we can say that ABCD is a rhombus.
Solution 19
Consider ABCD is a kite.
Then, AB = AD and BC = DC
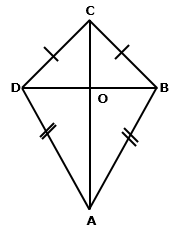

Solution 20


