FRANK Solutions for Class 9 Maths Chapter 25 - Surface Areas and Volume of Solids

Build your exam confidence with Frank Solutions for ICSE Class 9 Mathematics Chapter 25 Surface Areas and Volume of Solids. Can you comfortably find the surface area of a cube? Will you be able to confidently calculate the volume of air in a room as per given data? If these questions give you the exam jitters, you can regain your confidence by referring to our textbook solutions to attempt questions on surface areas and volume of solids with.

Also, practise solving problems such as finding the area of a cross section of a piece of metal or calculating the amount of water needed to fill a pool. Apart from TopperLearning’s ICSE Class 9 Maths Frank solutions, revise Maths problems from our Selina solutions for thorough exam preparation.

Read  more
Page / Exercise

Chapter 25 - Surface Areas and Volume of Solids Ex. 25.1

Solution 1

Solution 2

 

Solution 3

 

Solution 5

 

Volume of a cuboid = l x b x h

---------------------2400 = 20 × 15 × h

---------------------------h = 8 cm

Hence, height of the cuboid is 8 cm.

Solution 11

Volume of the square plate = Volume of a cuboid

   

 

 

  

 

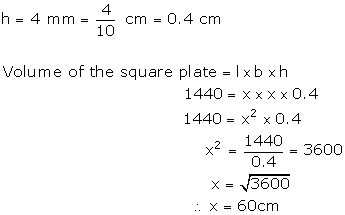
Solution 14

 

 

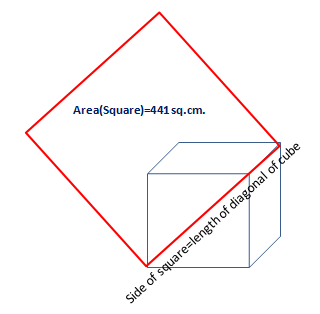
Solution 21

Solution 22

Solution 23

    

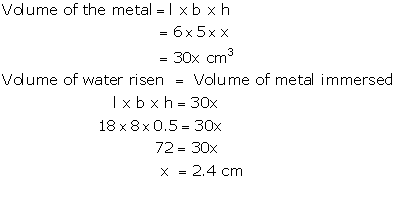
Solution 24

 

Solution 30

 

Solution 32

Solution 36

 

Solution 39

Solution 4
Solution 6
Solution 7
Solution 8
Solution 10
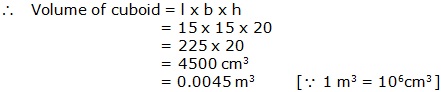
Solution 12
Solution 13
Solution 15
Solution 16
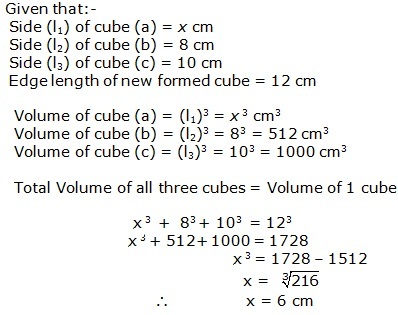
Solution 17
Solution 26
Solution 27
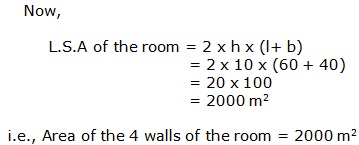
Solution 28
Solution 33
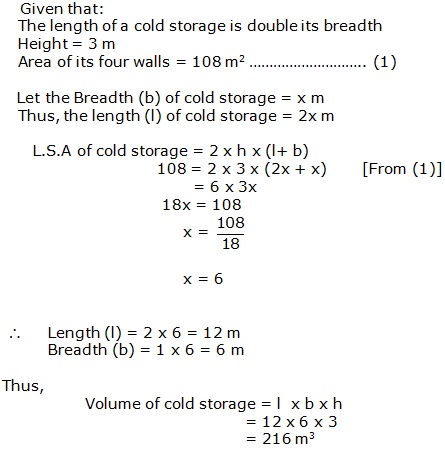
Solution 34
Solution 35

Chapter 25 - Surface Areas and Volume of Solids Ex. 25.2

Solution 12

Solution 13

Solution 15

Solution 23

Solution 25

 

Solution 26

 

Solution 27

   

Solution 28

Solution 29

Solution 30

Solution 31

Solution 1
Solution 2

Solution 3
Solution 4
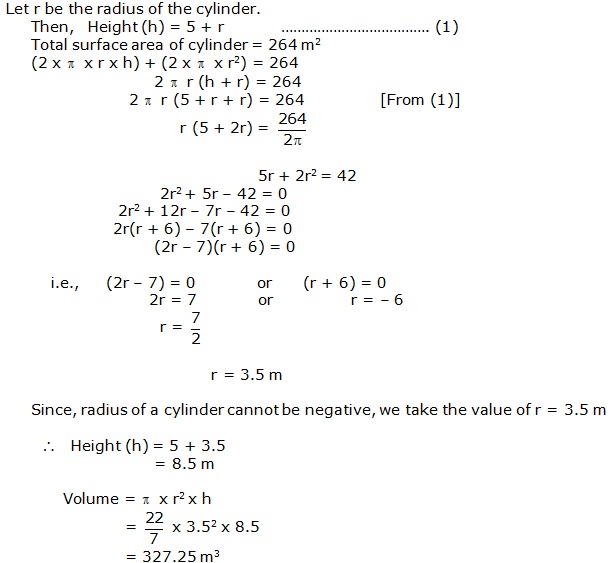
Solution 5
Solution 6
Solution 7
Solution 9
Solution 10
Solution 11
Solution 16
Solution 17

Solution 18
Solution 19
Solution 20
Solution 21

Chapter 25 - Surface Areas and Volume of Solids Ex. 25.3

Solution 1

 

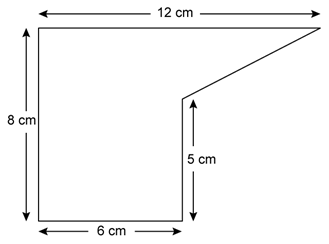
Solution 2

Solution 3

 

 

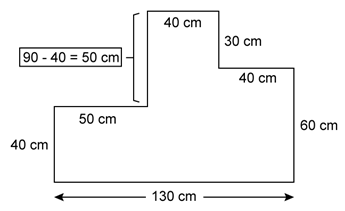
Solution 4

Solution 5

 

 

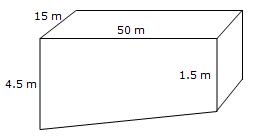
Solution 6

Solution 7

Solution 8

 

 



 

 

 

 

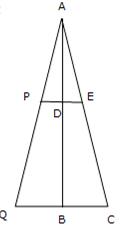
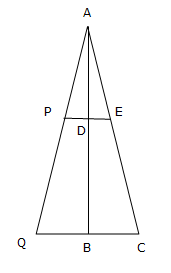
Solution 9

Solution 10

Solution 11

Solution 12

Solution 13

 

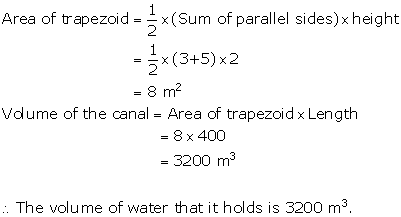
Solution 14

 

Solution 15