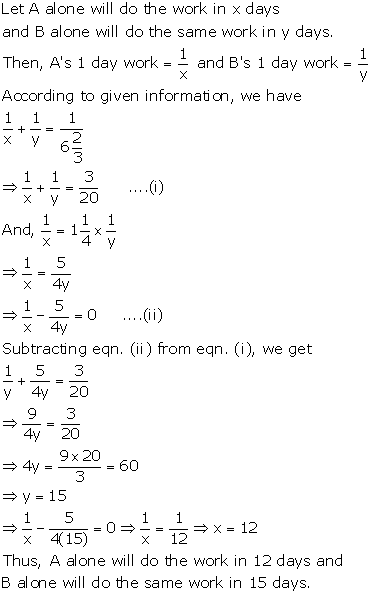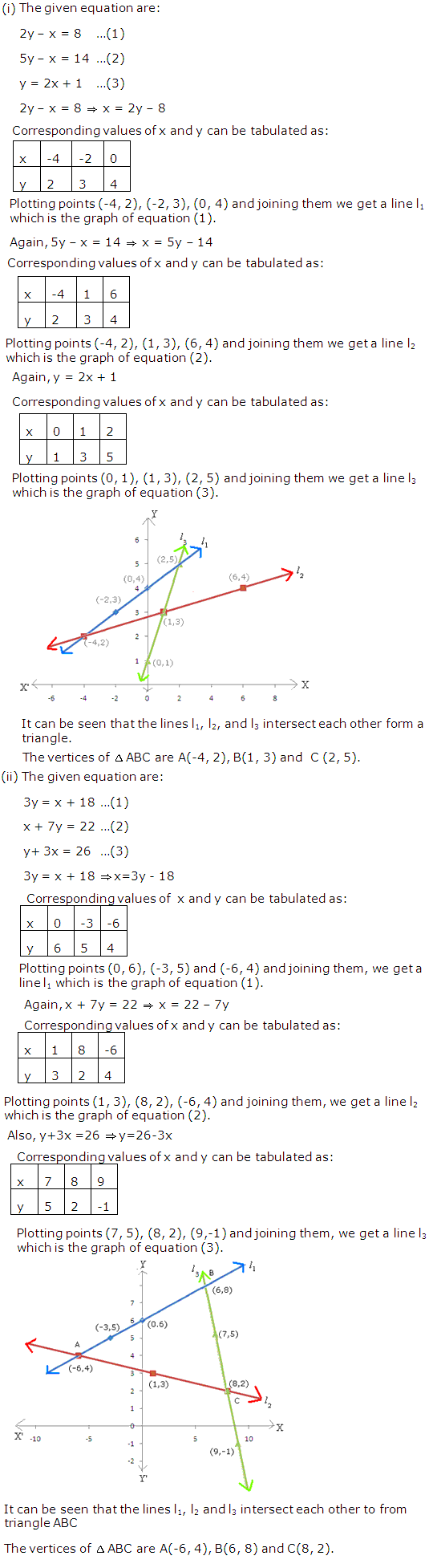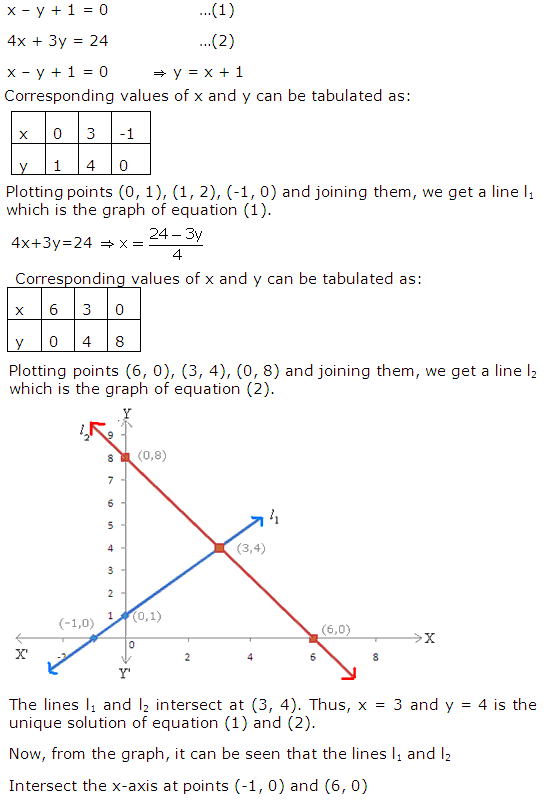Class 9 FRANK Solutions Maths Chapter 8 - Simultaneous Linear Equations
Solve equations confidently by practising Frank Solutions for ICSE Class 9 Mathematics Chapter 8 Simultaneous Linear Equations. Understand how to use graphical methods and linear equations to find the vertices of a given triangle. Take a closer look at the steps in our textbook solutions to understand how equations can be placed in a tabulated format to plot graphs and find answers.
You can use simultaneous linear equations to calculate income or find the cost of an item. To find out how, revise with the assistance of ICSE Class 9 Maths Frank textbook solutions at TopperLearning. If you have any doubts, post them on our study portal’s UnDoubt’ section for a response from our experts.
Simultaneous Linear Equations Exercise Ex. 8.1
Solution 1(a)
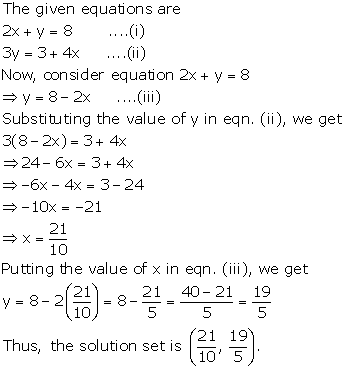
Solution 1(b)
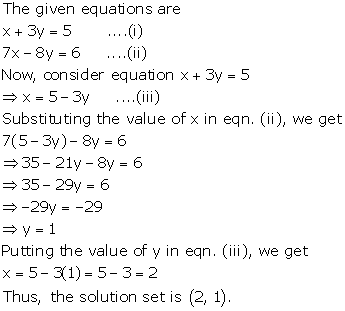
Solution 1(c)
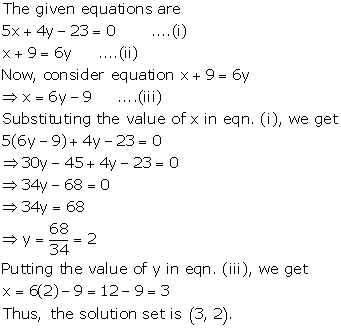
Solution 1(d)
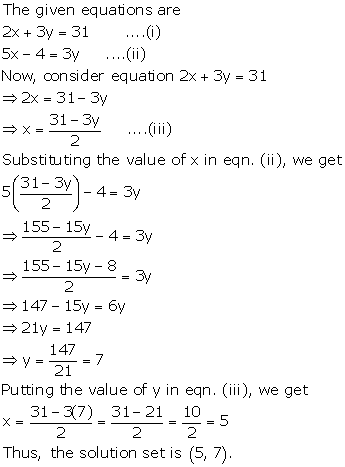
Solution 1(e)
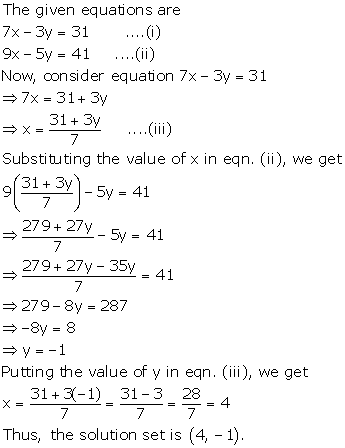
Solution 1(f)

Solution 1(g)

Solution 1(h)
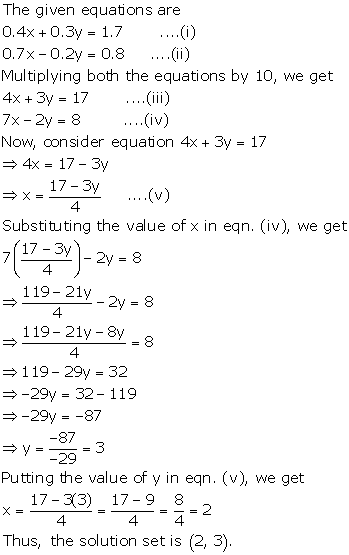
Solution 1(i)

Solution 1(j)
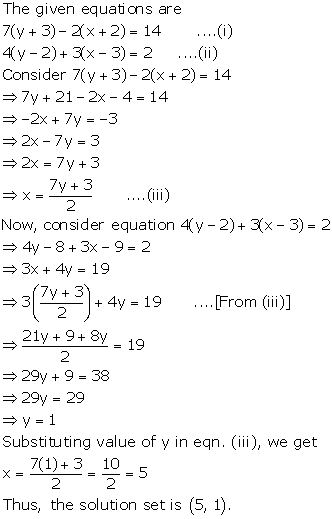
Solution 3(a)
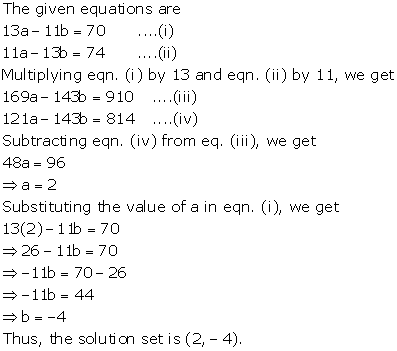
Solution 3(b)
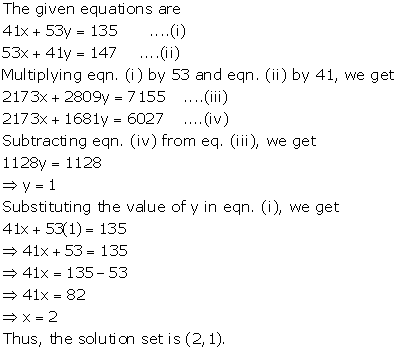
Solution 3(c)
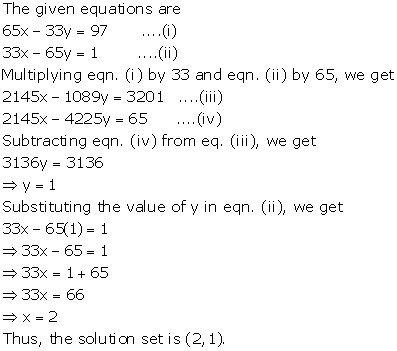
Solution 3(d)

Solution 4(a)
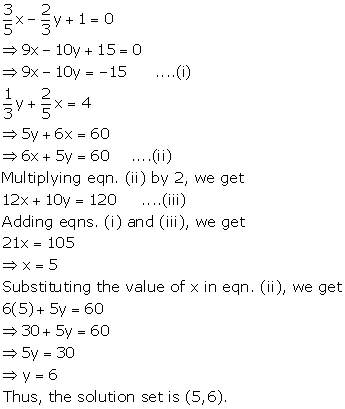
Solution 4(b)

Solution 4(c)

Solution 4(d)

Solution 4(e)
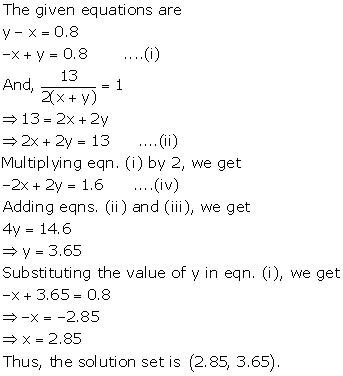
Solution 4(f)
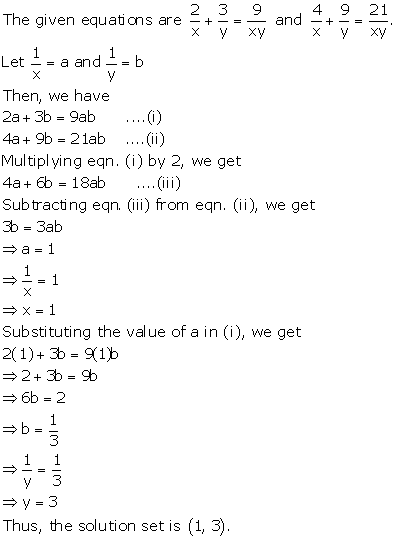
Solution 4(g)
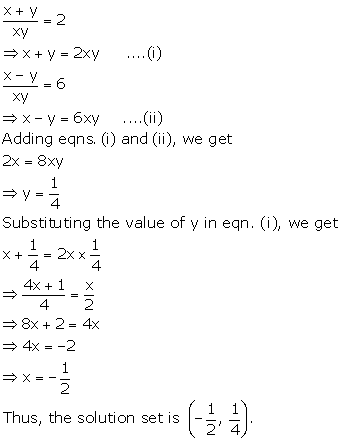
Solution 4(h)
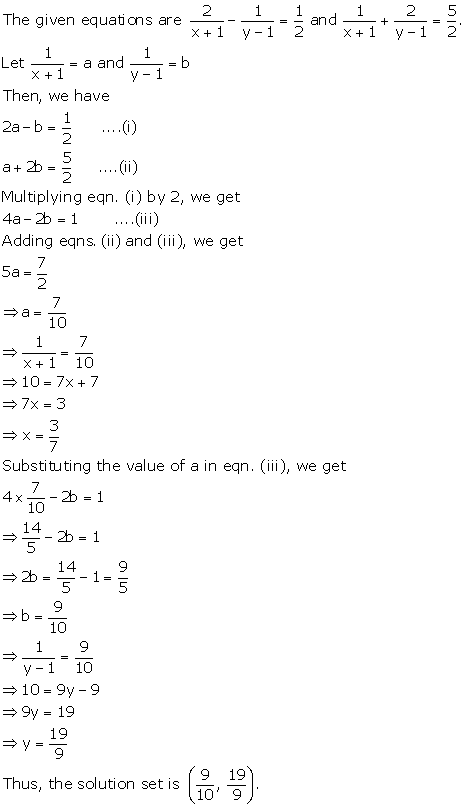
Solution 4(i)
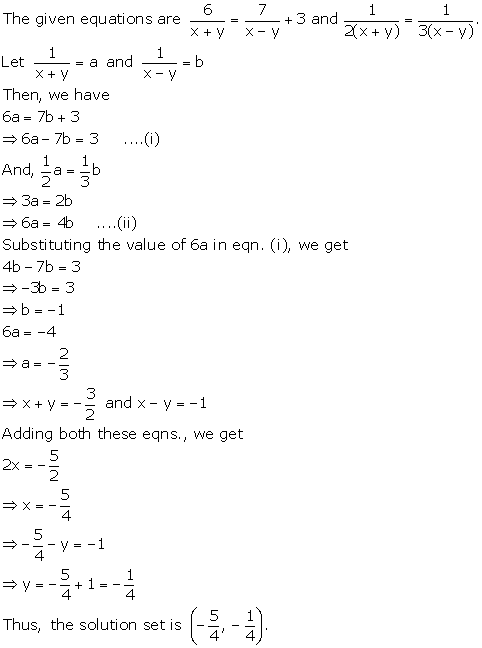
Solution 4(j)
Solution 4(k)

Solution 4(l)
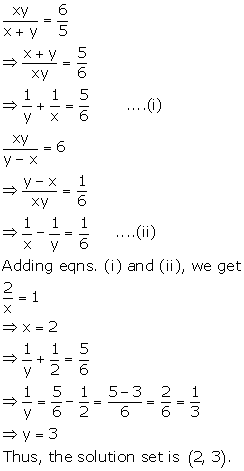
Solution 9
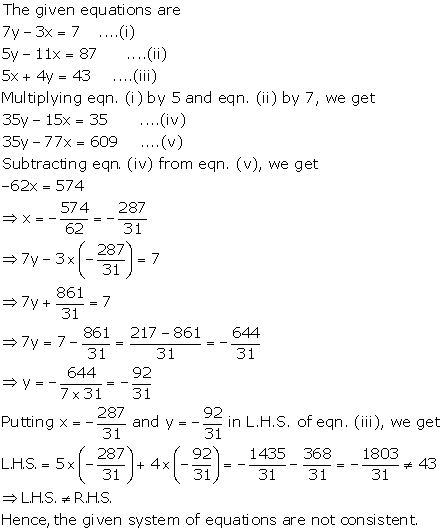
Solution 10
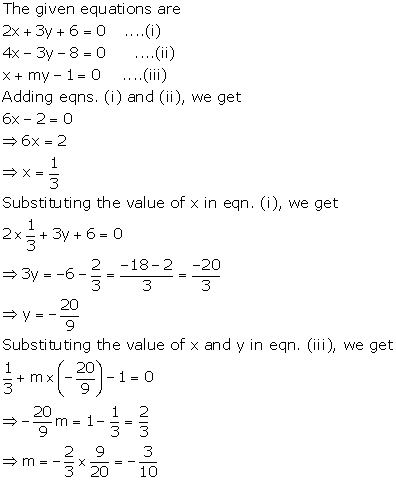
Solution 2
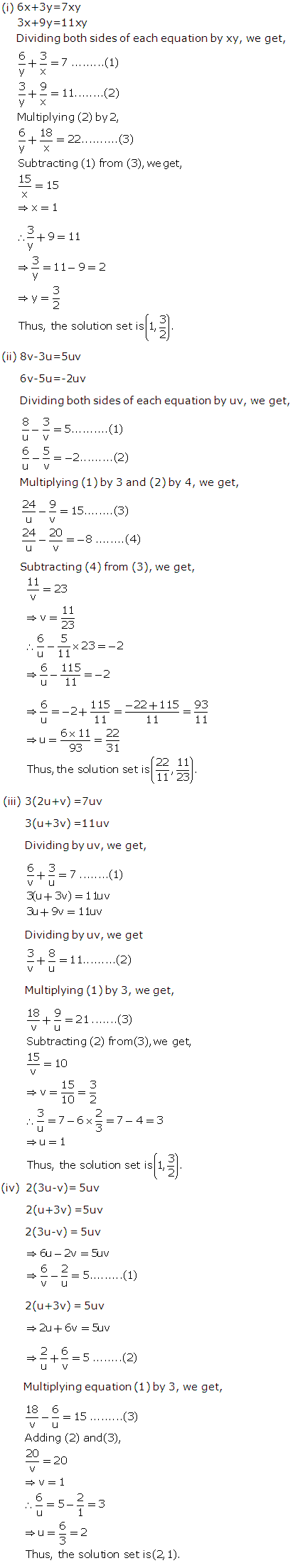
Solution 5
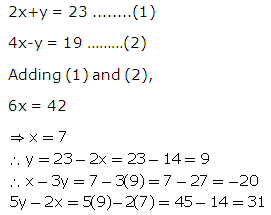
Solution 6
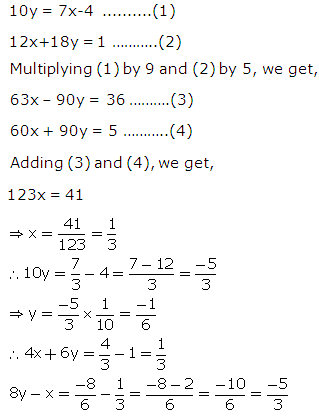
Solution 7
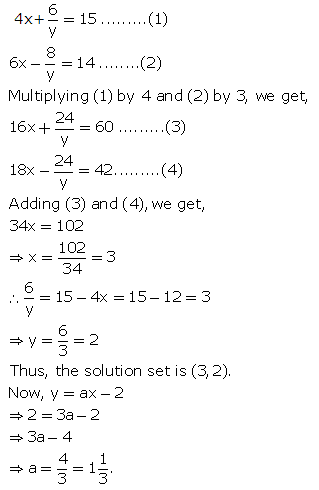
Solution 8

Simultaneous Linear Equations Exercise Ex. 8.2
Solution 1(a)
The graph of x = 3 is as follows:

Solution 1(b)
Given equation, y + 5 = 0
i.e. y = -5
The graph is as follows:
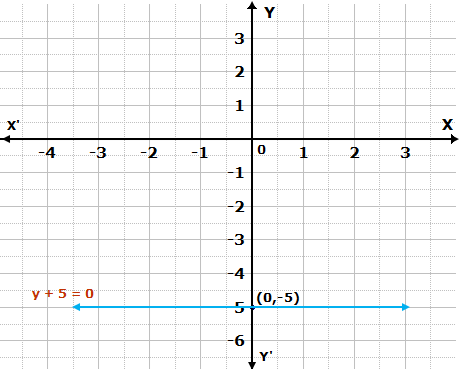
Solution 1(c)

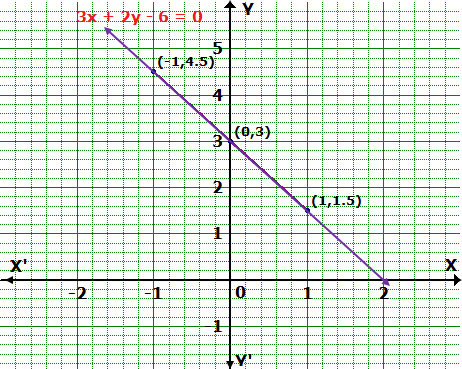
Solution 1(d)

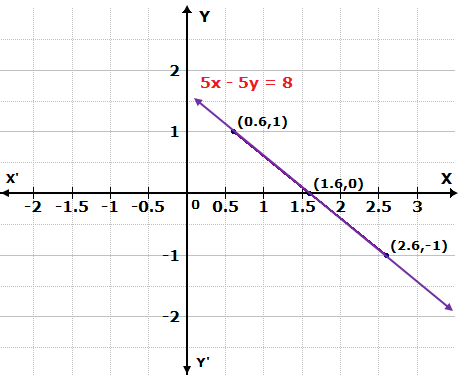
Solution 2(a)

Thus, the graph of the equation meets the X-axis at (2, 0) and Y-axis at (0, 3).
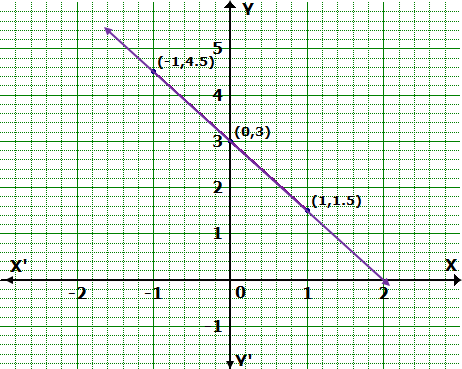
Solution 2(b)
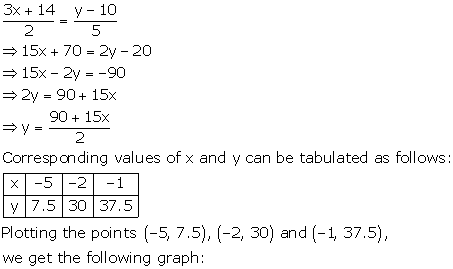
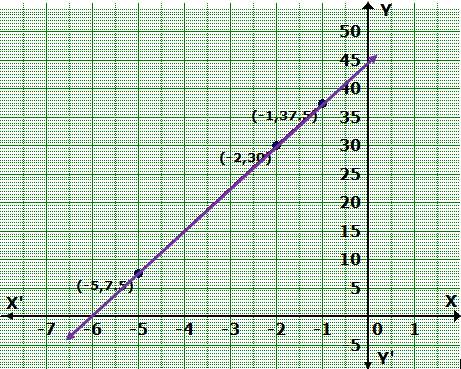
Thus, the graph of the equation meets the X-axis at (-6, 0) and Y-axis at (0, 45).
Solution 3

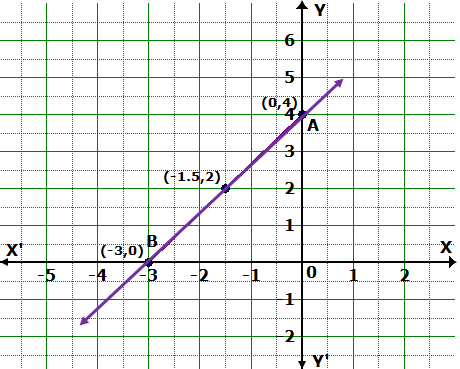
![]()
Solution 4
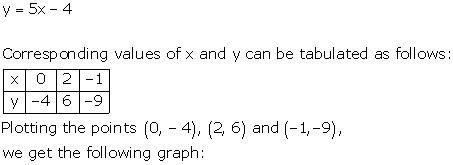
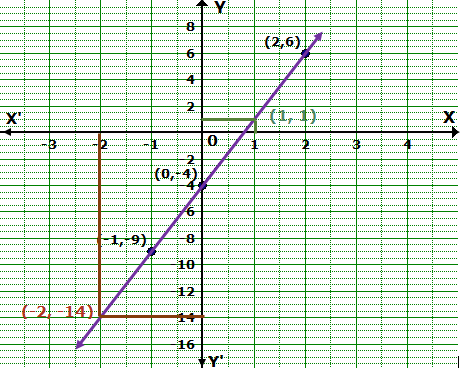
From the graph, we find that
a. When y = 1, x = 1.
b. When x = -2, y = -14
Solution 5
The graph is as follows:
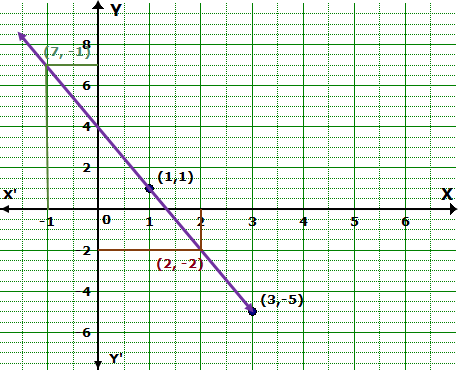
From the graph, we find that p = -1 and q = -2.
Solution 6
The graph is as follows:
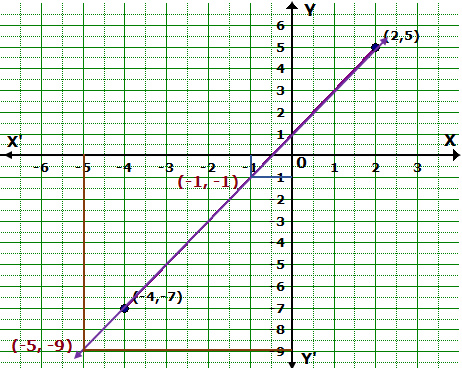
From the graph, we find that a = -1 and b = -9.
Solution 12(a)

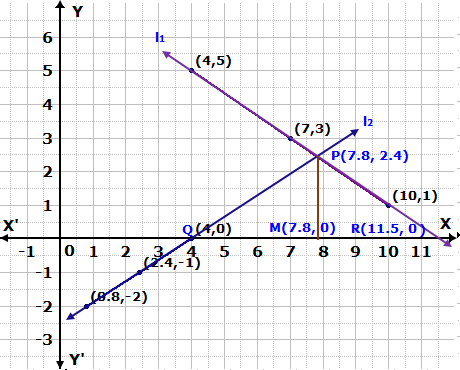

Solution 12(b)

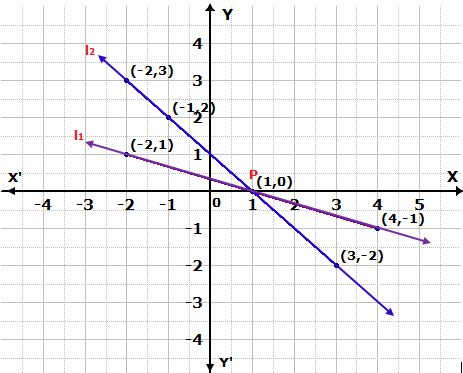

Solution 7

Solution 8
Solution 9
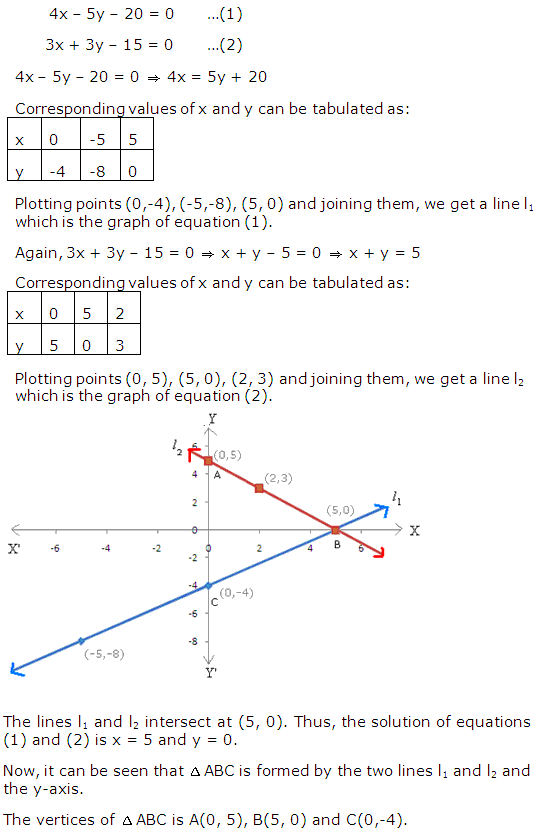
Solution 10
Solution 11
Simultaneous Linear Equations Exercise Ex. 8.3
Solution 1

Solution 2

Solution 3
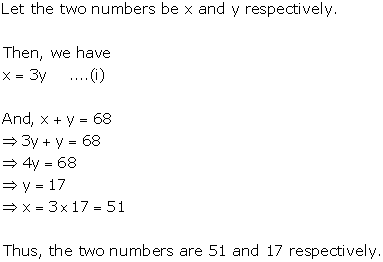
Solution 4

Solution 5

Solution 6

Solution 7

Solution 8

Solution 9

Solution 10

Solution 11

Solution 12

Solution 13

Solution 14

* Question modified
Solution 15

Solution 16
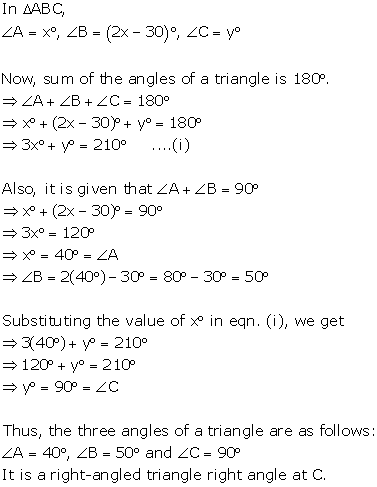
Solution 17

Solution 18

Solution 19

Solution 20

Solution 21

Solution 22

Solution 23

Solution 24

Solution 25

Solution 26

Solution 27

Solution 28

Solution 29