Class 9 FRANK Solutions Maths Chapter 17 - Pythagoras Theorem
Revise Frank Solutions for ICSE Class 9 Mathematics Chapter 17 Pythagoras Theorem on TopperLearning. As you revise, you may come across problems asking you to find the area of a right-angled triangle. The chapter solutions by our experts will help you use the Pythagoras theorem step-by-step to find the right answer.
Frank textbook solutions for ICSE Class 9 Maths also includes model answers on methods to find the length of the side of a triangle. Practise similar problems by going through our Selina solutions as well. For revisiting the basics, check our e-learning concept videos available 24x7 on our study portal.
Ex. 17.1
Pythagoras Theorem Exercise Ex. 17.1
Solution 12
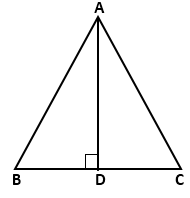
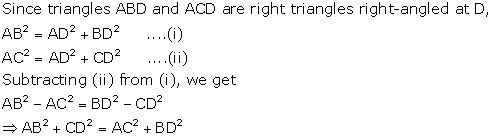
Solution 14
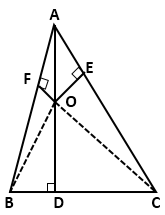

Solution 15



Solution 21


Solution 22
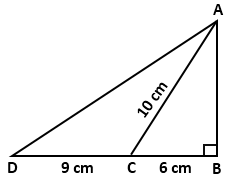

Solution 23
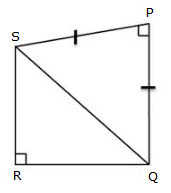

Solution 24
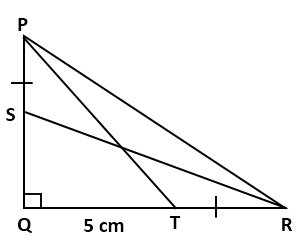

Solution 25
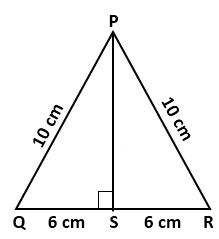

Solution 26
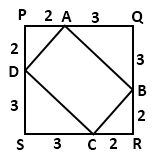
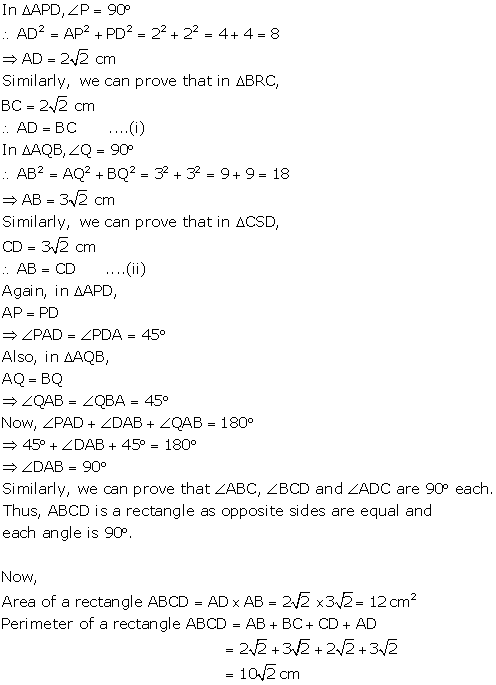
Solution 1
Solution 2
Solution 3
Solution 4
Solution 5
Solution 6
Solution 7
Solution 8
Solution 9
Solution 10

Solution 11
Solution 13
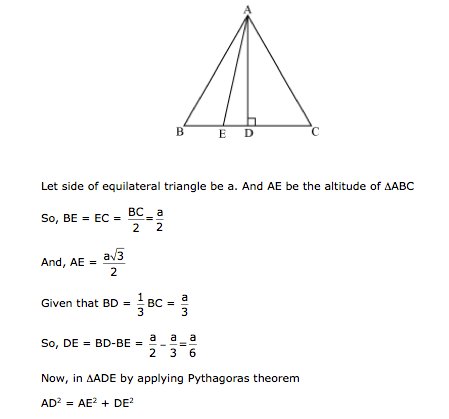
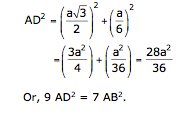
Solution 16
Solution 17
Solution 18
Solution 19
Solution 20
















