Class 9 FRANK Solutions Maths Chapter 10 - Logarithms
Revise textbook problems using Frank Solutions for ICSE Class 9 Mathematics Chapter 10 Logarithms available on TopperLearning. Learn the different laws of logarithm by practising the steps and applying them in Maths problems. Also, understand how to write complete steps to score good marks in logarithm-based problem with the help of our expertly created chapter solutions.
You can access the complete Frank textbook solutions for ICSE Class 9 Maths 24x7 online on the TopperLearning portal. Whether you want to practise the solutions to understand the methods of providing proofs or calculating values as per the type of question, you can do so at your convenience and your study schedule. The online availability of e-learning resources such as chapter solutions will help you quickly learning concepts with ease.
Logarithms Exercise Ex. 10.1
Solution 1

Solution 2

Solution 3

Solution 4

Solution 5

Solution 6

Solution 7

Solution 8

Solution 9

Solution 10

Logarithms Exercise Ex. 10.2
Solution 9
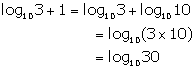
Solution 10(a)
False, since log xy = logx + logy
Solution 10(b)
True, since log 1= 0 and anything multiplied by 0 is 0.
Solution 10(c)
![]()
Solution 10(d)
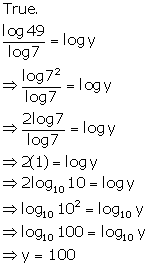
Solution 11(a)
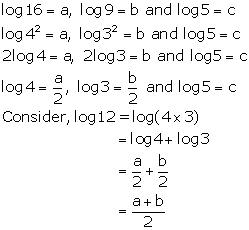
Solution 11(b)
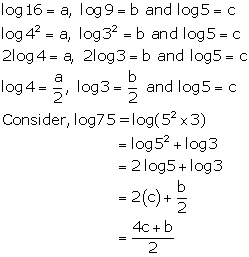
Solution 11(c)
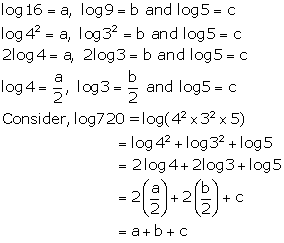
Solution 11(d)
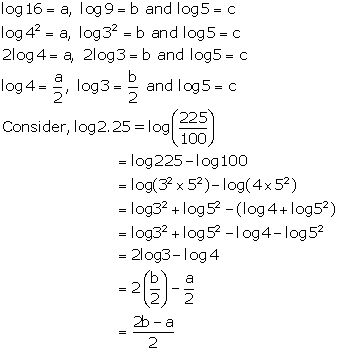
Solution 11(e)
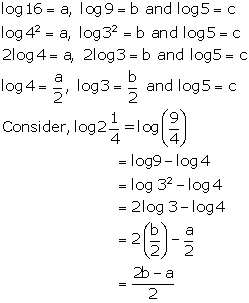
Solution 12
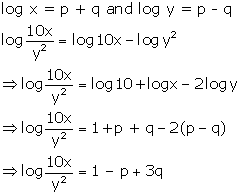
Solution 17(a)
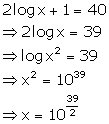
Solution 17(b)
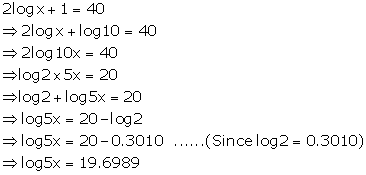
Solution 18(a)
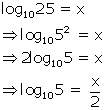
Solution 18(b)
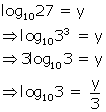
Solution 31(a)
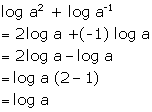
Solution 31(b)

Solution 32(a)
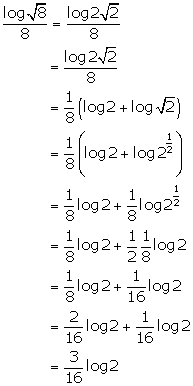
Solution 32(b)
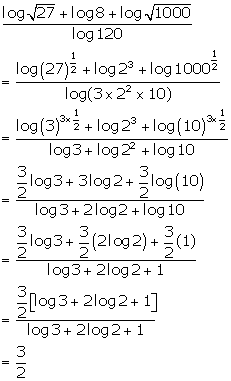
Solution 32(c)
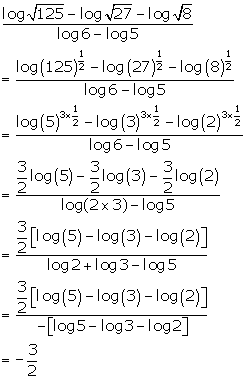
Solution 40
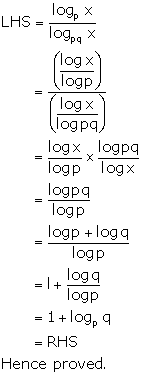
Solution 41(a)

Solution 41(b)

Solution 42
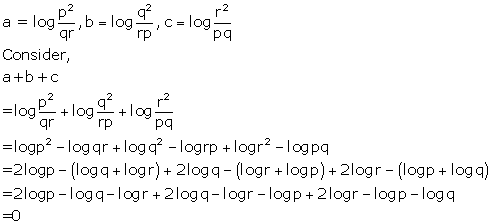
Solution 43
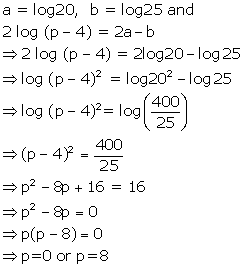
Solution 1
(vi)
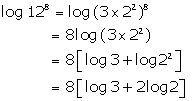
Solution 2
(vi)
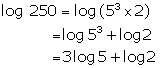
Solution 3
(vi)
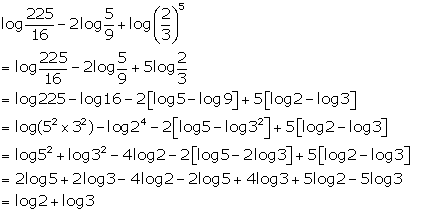
Solution 4
Solution 5
Solution 6
Solution 7
(viii)

Solution 8
Solution 13
Solution 14
Solution 15
Solution 16
Solution 19
Solution 20
Solution 21
Solution 22
Solution 23
Solution 24
Solution 25
Solution 26
Solution 27
Solution 28
Solution 29
Solution 30
Solution 33
Solution 34
Solution 35
Solution 36
Solution 37
Solution 38
Solution 39
































