Class 9 FRANK Solutions Maths Chapter 7 - Linear Equations
Study Frank Solutions for ICSE Class 9 Mathematics Chapter 7 Linear Equations to score more marks in your exam. Understand how to verify whether the given value is a solution of the given equation. Also, practise solving equations by using the method of collecting like terms.
In addition, revise TopperLearning’s Frank textbook solutions to use linear equations for calculating the distance travelled from one destination to another. If you are puzzled by linear equations, our ICSE Class 9 video lessons can be great help for strengthening your conceptual clarity. Also, browse our online practice tests and mock exam question papers for Maths practice.
Ex. 7.1
Ex. 7.2
Ex. 7.3
Ex. 7.4
Ex. 7.5
Ex. 7.6
Linear Equations Exercise Ex. 7.1
Solution 3(a)
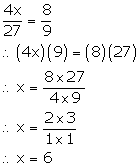
Solution 3(b)
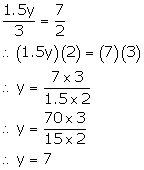
Solution 3(c)

Solution 3(d)
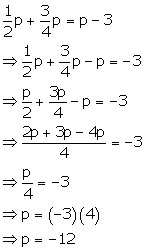
Solution 3(e)
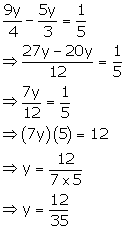
Solution 3(f)
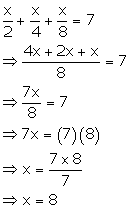
Solution 3(g)

Solution 3(h)
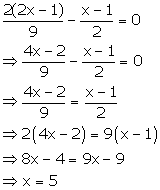
Solution 3(i)

Solution 3(j)

Solution 4(a)

Solution 4(b)
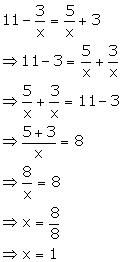
Solution 4(c)
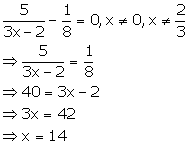
Solution 4(d)
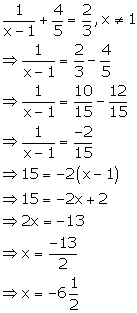
Solution 4(e)
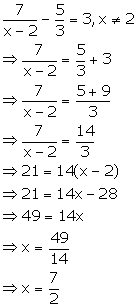
Solution 4(f)
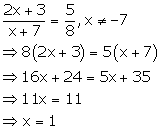
Solution 4(g)
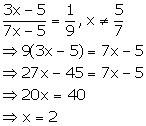
Solution 4(h)

Solution 4(i)
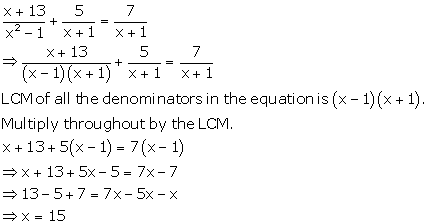
Solution 4(j)
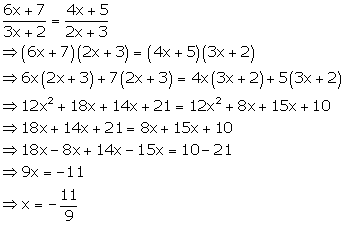
Solution 4(k)
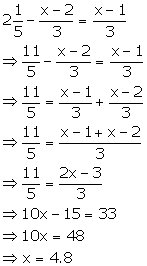
Solution 4(l)

Solution 4(m)
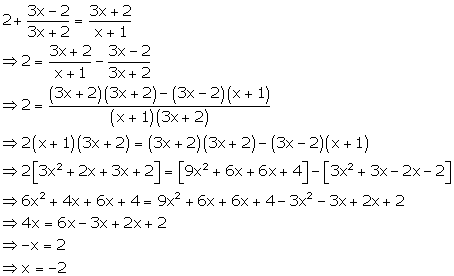
Solution 4(n)
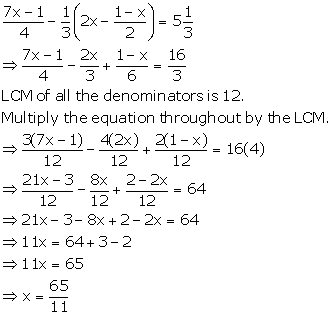
Solution 5(a)
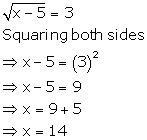
Solution 5(b)
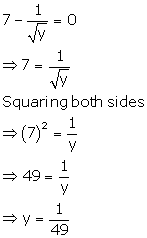
Solution 5(c)

Solution 5(d)
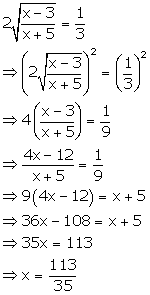
Solution 6
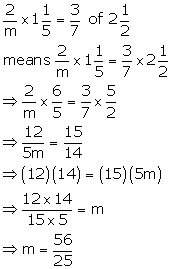
Solution 8
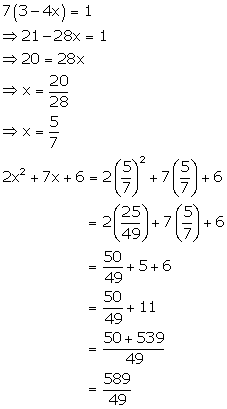
Solution 9
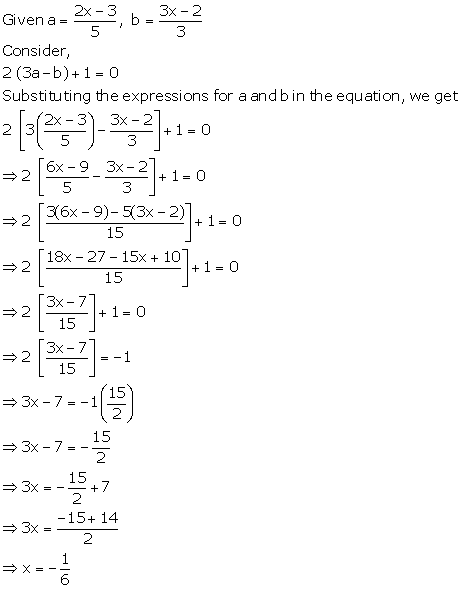
Solution 10
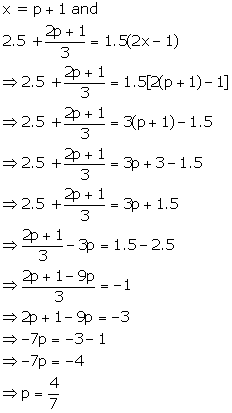
Solution 16

Solution 1
Solution 2
Solution 7
Solution 11
Solution 12
Solution 13
Solution 14
Solution 15
Linear Equations Exercise Ex. 7.2
Solution 19

Solution 23
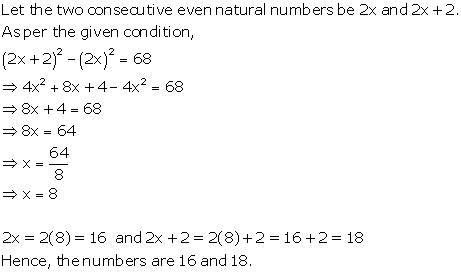
Solution 25
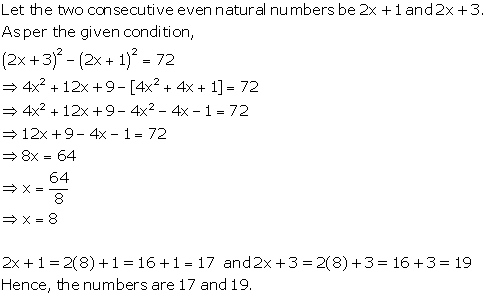
Solution 1

Solution 2

Solution 3

Solution 4

Solution 5

Solution 6

Solution 7

Solution 8
Solution 9
Solution 10
Solution 11
Solution 12
Solution 13
Solution 14
Solution 15
Solution 16
Solution 17
Solution 18
Solution 20
Solution 21
Solution 22
Solution 24
Solution 26
Solution 27
Solution 28
Linear Equations Exercise Ex. 7.3
Solution 11
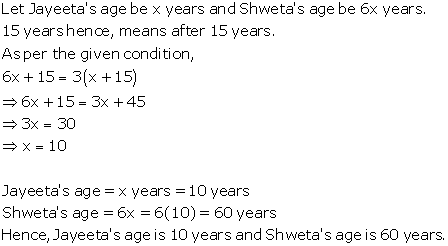
Solution 12
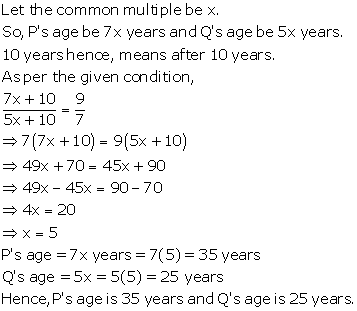
Solution 13
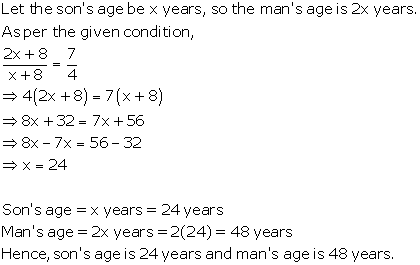
Solution 1
Solution 2
Solution 3
Solution 4
Solution 5
Solution 6
Solution 7
Solution 8
Solution 9
Solution 10
Linear Equations Exercise Ex. 7.4
Solution 1

Solution 2

Solution 3

Solution 4
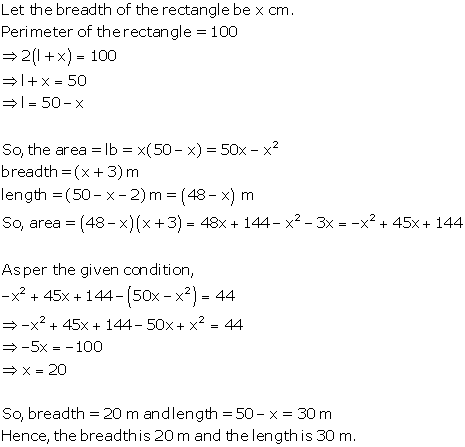
Solution 5

Solution 6

Solution 7

Solution 8
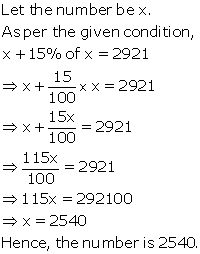
Solution 9
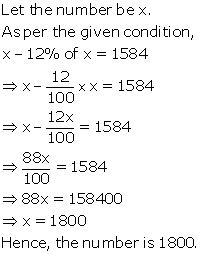
Solution 10
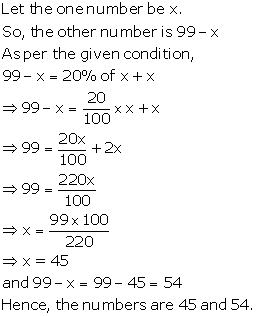
Solution 11

Solution 12
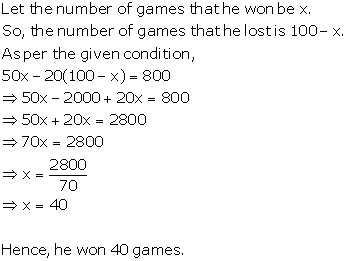
Solution 13

Solution 14

Solution 15

Solution 16

Solution 17

Solution 18

Solution 19

Linear Equations Exercise Ex. 7.5
Solution 1

Solution 2

Solution 3

Solution 4

Solution 5

Solution 6

Solution 7

Solution 8

Solution 9

Solution 10

Solution 11

Solution 12

Solution 13

Solution 14

Solution 15

Solution 16

Solution 17

Solution 18

Solution 19

Solution 20

Linear Equations Exercise Ex. 7.6
Solution 1

Solution 2

Solution 3

Solution 4

Solution 5

Solution 6

Solution 7

Solution 8

Solution 9

Solution 10

Solution 11

Solution 12

Solution 13

Solution 14

Solution 15

Solution 16

Solution 17

Solution 18

Solution 19

Solution 20






































