Class 9 FRANK Solutions Maths Chapter 13 - Inequalities in Triangles
How to show that the perimeter of a given triangle is more than the sum of its medians? Find answers in TopperLearning’s Frank solutions for ICSE Class 9 Mathematics Chapter 13 Inequalities in Triangles. Revise the application of properties of triangles to provide proofs in answers such as a particular side of an isosceles triangle is greater than another side.
Revise the Exterior Angle property, Angle Sum property and carious other properties of the triangle with our Frank textbook solutions. Practice makes you perfect; and that is why ICSE Class 9 Maths videos, online practice tests, and more study aids are at available on TopperLearning.
Ex. 13.1
Inequalities in Triangles Exercise Ex. 13.1
Solution 1(a)

Solution 1(b)

Solution 1(c)
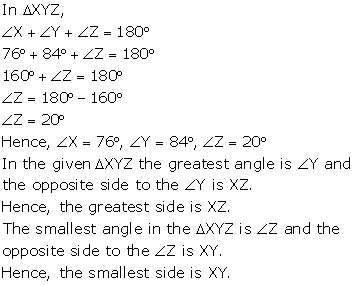
Solution 2(a)

Solution 2(b)

Solution 4

Solution 15

Solution 16

Solution 17(a)

Solution 17(b)

Solution 17(c)

Solution 18

Solution 19

Solution 20
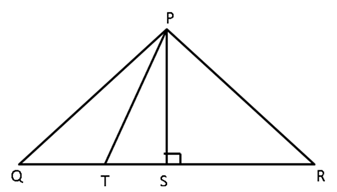
![]()

Solution 21

Solution 22

Solution 23
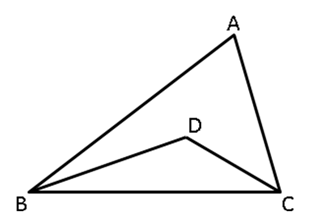

Solution 3

Solution 5
Solution 6
Solution 7
Solution 8
Solution 9
Solution 10
Solution 11
Solution 12
Solution 13
Solution 14











