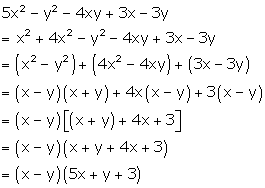FRANK Solutions for Class 9 Maths Chapter 5 - Factorisation
Achieve high marks with the support of Frank Solutions for ICSE Class 9 Mathematics Chapter 5 Factorisation. Prepared by TopperLearning’s experts, the solutions will help you understand how to factorise mathematical expressions by removing the common factors.
Also, learn the method of using the difference of two squares to factorise the given data. Explore ICSE Class 9 Maths Frank textbook solutions any time online on our online education portal. Additionally, with the help of our concept videos and online practice tests designed by subject experts, you can get ahead in your Maths learning.
Chapter 5 - Factorisation Exercise Ex. 5.1
Question 1(a)
Factorise the following by taking out the common factors:
4x2y3 - 6x3y2 - 12xy2
Solution 1(a)
Question 1(b)
Factorise the following by taking out the common factors:
5a(x2 - y2) + 35b(x2 - y2)
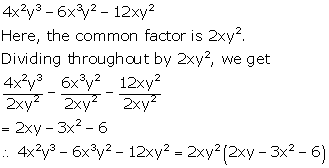
Solution 1(b)
Question 1(c)
Factorise the following by taking out the common factors:
2x5y + 8x3y2 - 12x2y3
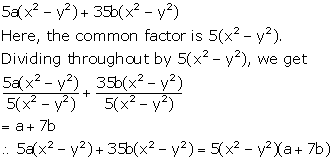
Solution 1(c)
Question 1(d)
Factorise the following by taking out the common factors:
12a3 + 15a2b - 21ab2
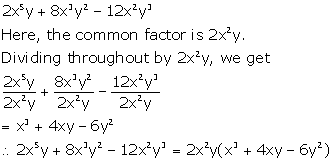
Solution 1(d)
Question 1(e)
Factorise the following by taking out the common factors:
24m4n6 + 56m6n4 - 72m2n2
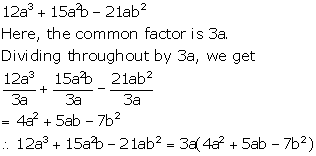
Solution 1(e)
Question 1(f)
Factorise the following by taking out the common factors:
(a - b)2 -2(a - b)
Solution 1(f)
Question 1(g)
Factorise the following by taking out the common factors:
2a(p2 + q2) + 4b(p2 + q2)
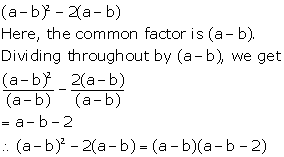
Solution 1(g)
Question 1(h)
Factorise the following by taking out the common factors:
81(p + q)2 -9p - 9q
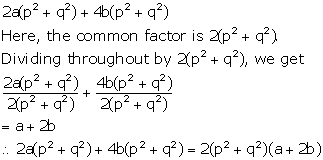
Solution 1(h)
Question 1(i)
Factorise the following by taking out the common factors:
(mx + ny)2 + (nx - my)2
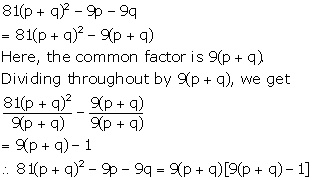
Solution 1(i)
Question 1(j)
Factorise the following by taking out the common factors:
36(x + y)3 - 54(x + y)2
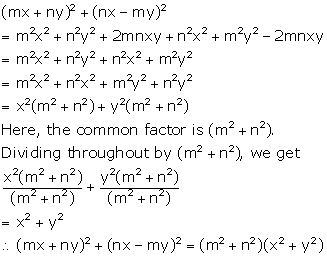
Solution 1(j)
Question 1(k)
Factorise the following by taking out the common factors:
p(p2 + q2 - r2) + q(r2 - q2 -p2) - r(p2 + q2 - r2)
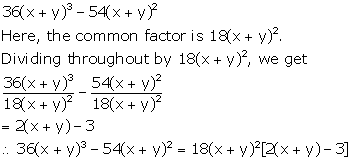
Solution 1(k)
Question 2(a)
Factorise the following by grouping the terms:
15xy - 9x - 25y + 15
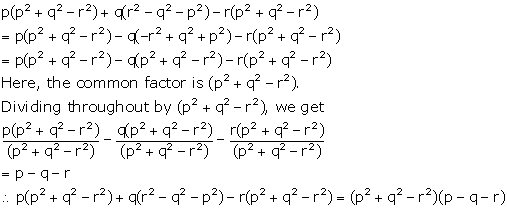
Solution 2(a)
15xy - 9x - 25y + 15
= (15xy - 9x) - (25y + 15)
= 3x(5y - 3) - 5(5y - 3)
= (5y - 3)(3x - 5)
Question 2(b)
Factorise the following by grouping the terms:
15x2 + 7y - 3x - 35xy
Solution 2(b)
15x2 + 7y - 3x - 35xy
= 15x2 - 3x - 35xy + 7y
= (15x2 - 3x) - (35xy - 7y)
= 3x(5x - 1) - 7y(5x - 1)
= (5x - 1)(3x - 7y)
Question 2(c)
Factorise the following by grouping the terms:
9 + 3xy + x2y + 3x
Solution 2(c)
9 + 3xy + x2y + 3x
= 9 + 3xy + 3x + x2y
= (9 + 3xy) + (3x + x2y)
= 3(3 + xy) + y(3 + xy)
= (3 + xy)(3 + x)
Question 2(d)
Factorise the following by grouping the terms:
8(2a + b)2 - 8a -4b
Solution 2(d)
8(2a + b)2 - 8a - 4b
= 8(2a + b)2 - (8a + 4b)
= 8(2a + b)2 - 4(2a + b)
= 4(2a + b)[2(2a + b) - 1]
= 4(2a + b)[4a + 2b - 1]
Question 2(e)
Factorise the following by grouping the terms:
x(x - 4)- x + 4
Solution 2(e)
x(x - 4) - x + 4
= x(x - 4) - 1(x - 4)
= (x - 4)(x - 1)
Question 2(f)
Factorise the following by grouping the terms:
2m3 - 5n2 - 5m2n + 2mn
Solution 2(f)
2m3 - 5n2 - 5m2n + 2mn
= 2m3 + 2mn - 5m2n - 5n2
= (2m3 + 2mn) - (5m2n + 5n2)
= 2m(m2 + n) - 5n(m2 + n)
= (m2 + n)(2m - 5n)
Question 2(g)
Factorise the following by grouping the terms:
4abx2 + 49aby2 + 14xy(a2 + b2)
Solution 2(g)
4abx2 + 49aby2 + 14xy(a2 + b2)
= 4abx2 + 49aby2 + 14a2xy + 14b2xy
= (4abx2 + 14a2xy) + (14b2xy + 49aby2)
= 2ax(2bx + 7ay) + 7by(2bx + 7ay)
= (2bx + 7ay)(2ax + 7by)
Question 2(h)
Factorise the following by grouping the terms:
9x3 + 6x2y2 - 4y3 - 6xy
Solution 2(h)
9x3 + 6x2y2 - 4y3 - 6xy
= 9x3 + 6x2y2 - 6xy - 4y3
= (9x3 + 6x2y2) - (6xy + 4y3)
= 3x2(3x + 2y2) - 2y(3x + 2y2)
= (3x + 2y2)(3x2 - 2y)
Question 2(i)
Factorise the following by grouping the terms:
3ax2 - 5bx2 + 9az2 + 6ay2 - 10by2 - 15bz2
Solution 2(i)
3ax2 - 5bx2 + 9az2 + 6ay2 - 10by2 - 15bz2
= 3ax2 + 6ay2 + 9az2 - 5bx2 - 10by2 - 15bz2
= (3ax2 + 6ay2 + 9az2) - (5bx2 + 10by2 + 15bz2)
= 3a(x2 + 2y2 + 3z2) - 5b(x2 + 2y2 + 3z2)
= (x2 + 2y2 + 3z2)(3a - 5b)
Question 2(j)
Factorise the following by grouping the terms:
8x3 - 24x2y + 54xy2 -162y3
Solution 2(j)
8x3 - 24x2y + 54xy2 - 162y3
= (8x3 - 24x2y) + (54xy2 - 162y3)
= 8x2(x - 3y) + 54y2(x - 3y)
= (x - 3y)(8x2 + 54y2)
Question 2(k)
Factorise the following by grouping the terms:
2a + b + 3c - d + (2a + b)3 + (2a + b)2(3c - d)
Solution 2(k)
2a + b + 3c - d + (2a + b)3 + (2a + b)2(3c - d)
= (2a + b + 3c - d) + [(2a + b)3 + (2a + b)2(3c - d)]
= 1(2a + b + 3c - d) + (2a + b)2(2a + b + 3c - d)
= (2a + b + 3c - d)[1 + (2a + b)2]
Question 2(l)
Factorise the following by grouping the terms:
xy(a2 + 1) + a(x2 + y2)
Solution 2(l)
xy(a2 + 1) + a(x2 + y2)
= a2xy + xy + ax2 + ay2
= (a2xy + ax2) + (ay2 + xy)
= ax(ay + x) + y(ay + x)
= (ay + x)(ax + y)
Question 2(m)
Factorise the following by grouping the terms:
p2x2 + (px2 + 1)x + p
Solution 2(m)
p2x2 + (px2 + 1)x + p
= p2x2 + px3 + x + p
= (p2x2 + px3) + (p + x)
= px2(p + x) + 1(p + x)
= (p + x)(px2 + 1)
Question 2(n)
Factorise the following by grouping the terms:
x2 - (p + q)x + pq
Solution 2(n)
x2 - (p + q)x + pq
= x2 - px - qx + pq
= (x2 - px) - (qx + pq)
= x(x - p) - q(x - p)
= (x - p)(x - q)
Question 2(o)
Factorise the following by grouping the terms:
Solution 2(o)
Question 2(p)
Factorise the following by grouping the terms:
x + y + m(x + y)
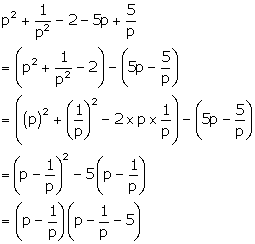
Solution 2(p)
x + y + m(x + y)
= (x + y) + m(x + y)
= (x + y)(1 + m)
Question 2(q)
Factorise the following by grouping the terms:
Solution 2(q)
Question 2(r)
Factorise the following by grouping the terms:
2p(a2 - 2b2) -14p + (a2 - 2b2)2 - 7(a2 - 2b2)
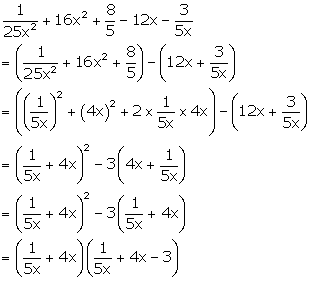
Solution 2(r)
2p(a2 - 2b2) - 14p + (a2 - 2b2)2 - 7(a2 - 2b2)
= 2p(a2 - 2b2) + (a2 - 2b2)2 - 14p - 7(a2 - 2b2)
= [2p(a2 - 2b2) + (a2 - 2b2)2] - [14p + 7(a2 - 2b2)]
= (a2 - 2b2)(2p + a2 - 2b2) - 7(2p + a2 - 2b2)
= (2p + a2 - 2b2)(a2 - 2b2 - 7)
Chapter 5 - Factorisation Exercise Ex. 5.2
Question 1(a)
Factorise the following by splitting the middle term:
x2 + 6x + 8
Solution 1(a)
x2 + 6x + 8
= x2 + 4x + 2x + 8
= x(x + 4) + 2(x + 4)
= (x + 4)(x + 2)
Question 1(b)
Factorise the following by splitting the middle term:
x2 - 11x + 24
Solution 1(b)
x2 - 11x + 24
= x2 - 8x - 3x + 24
= x(x - 8) - 3(x - 8)
= (x - 8)(x - 3)
Question 1(c)
Factorise the following by splitting the middle term:
x2 + 5x - 6
Solution 1(c)
x2 + 5x - 6
= x2 + 6x - x - 6
= x(x + 6) - 1(x + 6)
= (x + 6)(x - 1)
Question 1(d)
Factorise the following by splitting the middle term:
p2- 12p - 64
Solution 1(d)
p2 - 12p - 64
= p2 - 16p + 4p - 64
= p(p - 16) + 4(p - 16)
= (p - 16)(p + 4)
Question 1(e)
Factorise the following by splitting the middle term:
y2 - 2y - 24
Solution 1(e)
y2 - 2y - 24
= y2 - 6y + 4y - 24
= y(y - 6) + 4(y - 6)
=(y - 6)(y + 4)
Question 1(f)
Factorise the following by splitting the middle term:
3x2 + 19x - 14
Solution 1(f)
3x2 + 19x - 14
= 3x2 + 21x - 2x - 14
= 3x(x + 7) - 2(x + 7)
= (x + 7)(3x - 2)
Question 1(g)
Factorise the following by splitting the middle term:
15a2 - 14a - 16
Solution 1(g)
15a2 - 14a - 16
= 15a2 - 24a + 10a - 16
= 3a(5a - 8) + 2(5a - 8)
= (5a - 8)(3a + 2)
Question 1(h)
Factorise the following by splitting the middle term:
12 + x - 6x2
Solution 1(h)
12 + x - 6x2
= 12 + 9x - 8x - 6x2
= 3(4 + 3x) - 2x(4 + 3x)
= (4 + 3x)(3 - 2x)
Question 1(i)
Factorise the following by splitting the middle term:
7x2 + 40x - 12
Solution 1(i)
7x2 + 40x - 12
= 7x2 + 42x - 2x - 12
= 7x(x + 6) - 2(x + 6)
= (x + 6)(7x - 2)
Question 2(a)
Factorise the following:
5x2 - 17xy + 6y2
Solution 2(a)
5x2 - 17xy + 6y2
= 5x2 - 15xy - 2xy + 6y2
= 5x(x - 3y) - 2y(x - 3y)
= (x - 3y)(5x - 2y)
Question 2(b)
Factorise the following:
9x2 - 22xy + 8y2
Solution 2(b)
9x2 - 22xy + 8y2
= 9x2 - 18xy - 4xy + 8y2
= 9x(x - 2y) - 4y(x - 2y)
= (x - 2y)(9x - 4y)
Question 2(c)
Factorise the following:
2x3 + 5x2y - 12xy2
Solution 2(c)
2x3 + 5x2y - 12xy2
= 2x3 + 8x2y - 3x2y - 12xy2
= 2x2(x + 4y) - 3xy(x + 4y)
= (x + 4y)(2x2 - 3xy)
= (x + 4y)x(2x - 3y)
= x(x + 4y)(2x - 3y)
Question 2(d)
Factorise the following:
x2y2 + 15xy - 16
Solution 2(d)
x2y2 + 15xy - 16
= x2y2 + 16xy - xy - 16
= xy(xy + 16) - 1(xy + 16)
= (xy + 16)(xy - 1)
Question 2(e)
Factorise the following:
(2p + q)2 - 10p - 5q - 6
Solution 2(e)
(2p + q)2 - 10p - 5q - 6
= (2p + q)2 - (10p - 5q) - 6
= (2p + q)2 - 5(2p + q) - 6
= (2p + q)2 - 6(2p + q) + (2p + q) - 6
= (2p + q)(2p + q - 6) + 1(2p + q - 6)
= (2p + q - 6)(2p + q + 1)
Question 2(f)
Factorise the following:
y2 + 3y + 2 + by + 2b
Solution 2(f)
y2 + 3y + 2 + by + 2b
= y2 + y + 2y + 2 + by + 2b
= y2 + y + by + 2y + 2 + 2b
= y(y + 1 + b) + 2(y + 1 + b)
= (y + 1 + b)(y + 2)
Question 2(g)
Factorise the following:
x3y3 - 8x2y2 + 15xy
Solution 2(g)
x3y3 - 8x2y2 + 15xy
= x3y3 - 3x2y2 - 5x2y2 + 15xy
= x2y2(xy - 3) - 5xy(xy - 3)
= (xy - 3)(x2y2 - 5xy)
= (xy - 3)xy(xy - 5)
= xy(xy - 3)(xy - 5)
Question 2(h)
Factorise the following:
Solution 2(h)
Question 2(i)
Factorise the following:
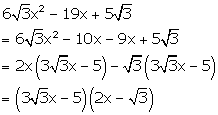
Solution 2(i)
Question 3(a)
Factorise the following:
5(3x + y)2 + 6(3x + y) - 8
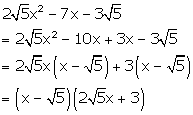
Solution 3(a)
5(3x + y)2 + 6(3x + y) - 8
= 5(3x + y)2 + 10(3x + y) - 4(3x + y) - 8
= 5(3x + y)(3x + y + 2) - 4(3x + y + 2)
= (3x + y + 2)[5(3x + y) - 4]
Question 3(b)
Factorise the following:
5 - 4(a - b) - 12(a - b)2
Solution 3(b)
5 - 4(a - b) - 12(a - b)2
= 5 - 10(a - b) + 6(a - b) - 12(a - b)2
= 5[1 - 2(a - b)] + 6(a - b)[1 - 2(a - b)]
= [5 + 6(a - b)][1 - 2(a - b)]
= (5 + 6a - 6b)(1 - 2a + 2b)
Question 3(c)
Factorise the following:
(3a - 2b)2 +3(3a - 2b) - 10
Solution 3(c)
(3a - 2b)2 + 3(3a - 2b) - 10
= (3a - 2b)2 + 5(3a - 2b) - 2(3a - 2b) - 10
= (3a - 2b)(3a - 2b + 5) - 2(3a - 2b +5)
= (3a - 2b + 5)((3a - 2b - 2)
Question 3(d)
Factorise the following:
(a2 - 2a)2 - 23(a2 - 2a) + 120
Solution 3(d)
(a2 - 2a)2 - 23(a2 - 2a) + 120
= (a2 - 2a)2 - 15(a2 - 2a) - 8(a2 - 2a) + 120
= (a2 - 2a)(a2 - 2a - 15) - 8(a2 - 2a - 15)
= (a2 - 2a - 15)(a2 - 2a - 8)
= (a2 - 5a + 3a - 15)(a2 - 4a + 2a - 8)
= [a(a - 5) + 3(a - 5)][a(a - 4) + 2(a - 4)]
= [(a - 5)(a + 3)][(a - 4)(a + 2)]
= (a - 5)(a + 3)(a - 4)(a + 2)
= (a + 2)(a + 3)(a - 4)(a - 5)
Question 3(e)
Factorise the following:
(x + 4)2 - 5xy - 20y - 6y2
Solution 3(e)
(x + 4)2 - 5xy - 20y - 6y2
= (x + 4)2 - 5y(x + 4) - 6y2
= (x + 4)2 - 6y(x + 4) + y(x + 4) - 6y2
= (x + 4)(x + 4 - 6y) + y(x + 4 - 6y)
= (x + 4 - 6y)(x + 4 + y)
= (x - 6y + 4)(x + y + 4)
Question 3(f)
Factorise the following:
7(x - 2)2 - 13(x - 2) - 2
Solution 3(f)
7(x - 2)2 - 13(x - 2) - 2
= 7(x - 2)2 - 14(x - 2) + (x - 2) - 2
= 7(x - 2)(x - 2 - 2) + 1(x - 2 - 2)
= 7(x - 2)(x - 4) + 1(x - 4)
= (x - 4)[7(x - 2) + 1]
= (x - 4)(7x - 14 + 1)
= (x - 4)(7x - 13)
Question 3(g)
Factorise the following:
12 - (y + y2)(8 - y - y2)
Solution 3(g)
12 - (y + y2)(8 - y - y2)
= 12 - a(8 - a) [Taking y + y2 = a]
= 12 - 8a + a2
= 12 - 6a - 2a + a2
= 6(2 - a) - a(2 - a)
= (2 - a)(6 - a)
= [2 - (y + y2)][6 - (y + y2)]
= (2 - y - y2)(6 - y - y2)
= (2 - 2y + y - y2)(6 - 3y + 2y - y2)
= [2(1 - y) + y(1 - y)][3(2 - y) + y(2 - y)]
= [(1 - y)(2 + y)][(2 - y)(3 + y)]
= (1 - y)(2 + y)(2 - y)(3 + y)
= (y - 1)(y + 2)(y - 2)(y + 3)
Question 3(h)
Factorise the following:
(p2 + p)2 - 8(p2 + p) + 12
Solution 3(h)
(p2 + p)2 - 8(p2 + p) + 12
= (p2 + p)2 - 6(p2 + p) - 2(p2 + p) + 12
= (p2 + p)(p2 + p - 6) - 2(p2 + p - 6)
= (p2 + p - 6)(p2 + p - 2)
= (p2 + 3p - 2p - 6)(p2 + 2p - p - 2)
= [p(p + 3) - 2(p + 3)][p(p + 2) - 1(p + 2)]
= [(p + 3)(p - 2)][(p + 2)(p - 1)]
= (p + 3)(p - 2)(p + 2)(p - 1)
Question 4(a)
Factorise the following:
(y2 - 3y)(y2 - 3y + 7) + 10
Solution 4(a)
(y2 - 3y)(y2 - 3y + 7) + 10
= a(a + 7) + 10 [taking (y2 - 3y) = a]
= a2 + 7a + 10
= a2 + 5a + 2a + 10
= a(a + 5) + 2(a + 5)
= (a + 5)(a + 2)
= (y2 - 3y + 5)(y2 - 3y + 2)
= (y2 - 3y + 5)(y2 - 2y - y + 2)
= (y2 - 3y + 5)[y(y - 2) - 1(y - 2)]
= (y2 - 3y + 5)[(y - 2)(y - 1)]
= (y - 1)(y - 2)(y2 - 3y + 5)
Question 4(b)
Factorise the following:
(t2 - t)(4t2 - 4t - 5) - 6
Solution 4(b)
(t2 - t)(4t2 - 4t - 5) - 6
= (t2 - t)[4(t2 - t) - 5] - 6
= a[4a - 5] - 6 [Taking (t2 - t) = a]
= 4a2 - 5a - 6
= 4a2 - 8a + 3a - 6
= 4a(a - 2) + 3(a - 2)
= (a - 2)(4a + 3)
= (t2 - t - 2)[4(t2 - t) + 3]
= (t2 - 2t + t - 2)(4t2 - 4t + 3)
= [t(t - 2) + 1(t - 2)](4t2 - 4t + 3)
= [(t - 2)(t + 1)](4t2 - 4t + 3)
= (t + 1)(t - 2)(4t2 - 4t + 3)
Question 4(c)
Factorise the following:
12(2x - 3y)2 - 2x + 3y - 1
Solution 4(c)
12(2x - 3y)2 - 1(2x - 3y) - 1
= 12a2 - a - 1 [Taking (2x - 3y) = a]
= 12a2 - 4a + 3a - 1
= 4a(3a - 1) + 1(3a - 1)
= (3a - 1)(4a + 1)
= [3(2x - 3y) - 1][4(2x - 3y) + 1]
= (6x - 9y - 1)(8x - 12y + 1)
Question 4(d)
Factorise the following:
6 - 5x + 5y + (x - y)2
Solution 4(d)
6 - 5x + 5y + (x - y)2
= 6 - 5(x - y) + (x - y)2
= 6 - 3(x - y) - 2(x - y) + (x - y)2
= 3[2 - (x - y)] - (x - y)[2 - (x - y)]
= 3(2 - x + y) - (x - y)(2 - x + y)
= (2 - x + y)(3 - x + y)
Question 4(e)
Factorise the following:
Solution 4(e)
Question 4(f)
Factorise the following:
p4 + 23p2q2 + 90q4
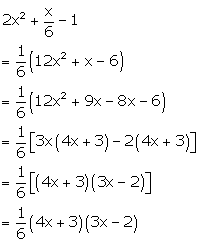
Solution 4(f)
P4 + 23p2q2 + 90q4
= p4 + 18p2q2 + 5p2q2 + 90q4
= p2(p2 + 18q2) + 5q2(p2 + 18q2)
= (p2 + 18q2)(p2 + 5q2)
Question 4(g)
Factorise the following:
2a3 + 5a2b - 12ab2
Solution 4(g)
2a3 + 5a2b - 12ab2
= 2a3 + 8a2b - 3a2b - 12ab2
= 2a2(a + 4b) - 3ab(a + 4b)
= (a + 4b)(2a2 - 3ab)
= (a + 4b)a(2a - 3b)
= a(a + 4b)(2a - 3b)
Chapter 5 - Factorisation Exercise Ex. 5.3
Question 1(a)
Factorise the following by the difference of two squares:
x2 - 16
Solution 1(a)
x2 - 16
= x2 - 42
= (x - 4)(x + 4)
Question 1(b)
Factorise the following by the difference of two squares:
64x2 - 121y2
Solution 1(b)
64x2 - 121y2
= (8x)2 - (11y)2
= (8x - 11y)(8x + 11y)
Question 1(c)
Factorise the following by the difference of two squares:
441 - 81y2
Solution 1(c)
441 - 81y2
= (21)2 - (9y)2
= (21 - 9y)(21 + 9y)
= 3(7 - 3y)3(7 + 3y)
= 9(7 - 3y)(7 + 3y)
Question 1(d)
Factorise the following by the difference of two squares:
x6 - 196
Solution 1(d)
x6 - 196
= (x3)2 - (14)2
= (x3 - 14)(x3 + 14)
Question 1(e)
Factorise the following by the difference of two squares:
625 - b2
Solution 1(e)
625 - b2
= (25)2 - (b)2
= (25 - b)(25 + b)
Question 1(f)
Factorise the following by the difference of two squares:
Solution 1(f)
Question 1(g)
Factorise the following by the difference of two squares:
8xy2 - 18x3
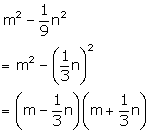
Solution 1(g)
8xy2 - 18x3
= 2x(4y2 - 9x2)
= 2x[(2y)2 - (3x)2]
= 2x[(2y - 3x)(2y + 3x)]
= 2x(2y - 3x)(2y + 3x)
Question 1(h)
Factorise the following by the difference of two squares:
16a4 - 81b4
Solution 1(h)
16a4 - 81b4
= (4a2)2 - (9b2)2
= (4a2 - 9b2)(4a2 + 9b2)
= [(2a)2 - (3b)2](4a2 + 9b2)
= [(2a - 3b)(2a + 3b)](4a2 + 9b2)
= (2a - 3b)(2a + 3b)(4a2 + 9b2)
Question 1(i)
Factorise the following by the difference of two squares:
a(a - 1) - b(b - 1)
Solution 1(i)
a(a - 1) - b(b - 1)
= a2 - a - b2 + b
= a2 - b2 - a + b
= (a2 - b2) - (a - b)
= (a - b)(a + b) - (a - b)
= (a - b)(a + b - 1)
Question 1(j)
Factorise the following by the difference of two squares:
(x + y)2 -1
Solution 1(j)
(x + y)2 - 1
= (x + y)2 - (1)2
= (x + y + 1)(x + y - 1)
Question 1(k)
Factorise the following by the difference of two squares:
x2 + y2 - z2 - 2xy
Solution 1(k)
x2 + y2 - z2 - 2xy
= x2 + y2 - 2xy - z2
= (x2 + y2 - 2xy) - z2
= (x - y)2 - (z)2
= (x - y - z)(x - y + z)
Question 1(l)
Factorise the following by the difference of two squares:
(x - 2y)2 -z2
Solution 1(l)
(x - 2y)2 - z2
= (x - 2y)2 - (z)2
= (x - 2y - z)(x - 2y + z)
Question 2(a)
Factorise the following:
9(a - b)2 - (a + b)2
Solution 2(a)
9(a - b)2 - (a + b)2
= [3(a - b)]2 - (a + b)2
= [3(a - b) - (a + b)][3(a - b) + (a + b)]
= (3a - 3b - a - b)(3a - 3b + a + b)
= (2a - 4b)(4a - 2b)
= 2(a - 2b)2(2a - b)
= 4(a - 2b)(2a - b)
Question 2(b)
Factorise the following:
25(x - y)2 - 49(c - d)2
Solution 2(b)
25(x - y)2 - 49(c - d)2
= [5(x - y)]2 - [7(c - d)]2
= [5(x - y) - 7(c - d)][5(x - y) + 7(c - d)]
= (5x - 5y - 7c + 7d)(5x - 5y + 7c - 7d)
Question 2(c)
Factorise the following:
(2a - b)2 -9(3c - d)2
Solution 2(c)
(2a - b)2 - 9(3c - d)2
= (2a - b)2 - [3(3c - d)]2
= [(2a - b) - 3(3c - d)][(2a - b) + 3(3c - d)]
= (2a - b - 9c + 3d)(2a - b + 9c - 3d)
Question 2(d)
Factorise the following:
b2 - 2bc + c2 - a2
Solution 2(d)
b2 - 2bc + c2 - a2
= (b2 - 2bc + c2) - a2
= (b - c)2 - (a)2
= (b - c - a)(b - c + a)
Question 2(e)
Factorise the following:
Solution 2(e)
Question 2(f)
Factorise the following:
(x2 + y2 - z2)2 - 4x2y2
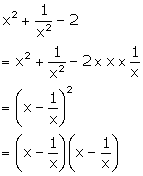
Solution 2(f)
(x2 + y2 - z2)2 - 4x2y2
= (x2 + y2 - z2)2 - (2xy)2
= (x2 + y2 - z2 - 2xy)(x2 + y2 - z2 + 2xy)
= [(x2 + y2 - 2xy) - z2][(x2 + y2 + 2xy) - z2]
= [(x - y)2 - z2][(x + y)2 - z2]
= [(x - y - z)(x - y + z)][(x + y - z)(x + y + z)]
= (x - y - z)(x - y + z)(x + y - z)(x + y + z)
Question 2(g)
Factorise the following:
a2 + b2 - c2 - d2 + 2ab - 2cd
Solution 2(g)
a2 + b2 - c2 - d2 + 2ab - 2cd
= (a2 + b2 + 2ab) - (c2 + d2 + 2cd)
= (a + b)2 - (c + d)2
= (a + b + c + d)(a + b - c - d)
Question 2(h)
Factorise the following:
4xy - x2 - 4y2 + z2
Solution 2(h)
4xy - x2 - 4y2 + z2
= z2 - x2 - 4y2 + 4xy
= z2 - (x2 + 4y2 - 4xy)
= z2 - (x - 2y)2
= [z - (x - 2y)][z + (x - 2y)]
= (z - x + 2y)(z + x - 2y)
Question 2(i)
Factorise the following:
4x2 - 12ax - y2 - z2 - 2yz + 9a2
Solution 2(i)
4x2 - 12ax - y2 - z2 - 2yz + 9a2
= (4x2 - 12ax + 9a2) - (y2 + z2 + 2yz)
= (2x - 3a)2 - (y + z)2
= [(2x - 3a) + (y + z)][(2x - 3a) - (y + z)]
= (2x - 3a + y + z)(2x - 3a - y - z)
Question 2(j)
Factorise the following:
(x + y)3 - x - y
Solution 2(j)
(x + y)3 - x - y
= (x + y)(x + y)2 - (x + y)
= (x + y)[(x + y)2 - 1]
= (x + y)[(x + y + 1)(x + y - 1)]
= (x + y)(x + y + 1)(x + y - 1)
Question 2(k)
Factorise the following:
y4 + y2 + 1
Solution 2(k)
y4 + y2 + 1
= y4 + 2y2 + 1 - y2
= (y2 + 1)2 - y2
= (y2 + 1 + y)(y2 + 1 - y)
Question 2(l)
Factorise the following:
(a2 - b2)(c2 - d2) - 4abcd
Solution 2(l)
(a2 - b2)(c2 - d2) - 4abcd
= a2c2 - a2d2 - b2c2 + b2d2 - 4abcd
= a2c2 + b2d2 - 2abcd - a2d2 - b2c2 - 2abcd
= (a2c2 + b2d2 - 2abcd) - (a2d2 + b2c2 + 2abcd)
= (ac - bd)2 - (ad + bc)2
= [(ac - bd) + (ad + bc)][(ac - bd) - (ad + bc)]
= (ac - bd + ad + bc)(ac - bd - ad - bc)
Question 3(a)
Express each of the following as the difference of two squares:
(x2 - 2x + 3)(x2 + 2x + 3)
Solution 3(a)
Question 3(b)
Express each of the following as the difference of two squares:
(x2 - 2x + 3) (x2 - 2x - 3)
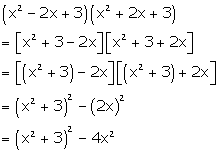
Solution 3(b)
Question 3(c)
Express each of the following as the difference of two squares:
(x2 + 2x - 3) (x2 - 2x + 3)
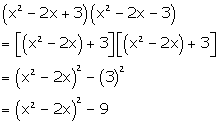
Solution 3(c)
Question 4(a)
Factorise:
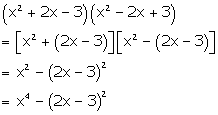
Solution 4(a)
Question 4(b)
Factorise:
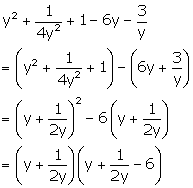
Solution 4(b)
Question 4(c)
Factorise:
x4 + y4 - 6x2y2
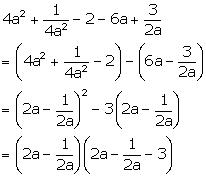
Solution 4(c)
Question 4(d)
Factorise:
4x4 + 25y4 + 19x2y2
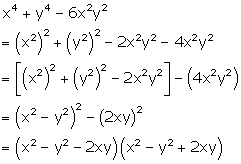
Solution 4(d)
Question 4(e)
Factorise:
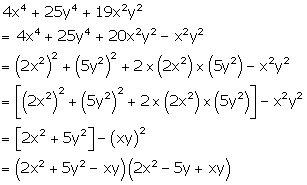
Solution 4(e)
Question 4(f)
Factorise:
5x2 - y2 - 4xy + 3x - 3y
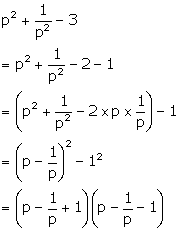
Solution 4(f)
Kindly Sign up for a personalised experience
- Ask Study Doubts
- Sample Papers
- Past Year Papers
- Textbook Solutions
Sign Up
Verify mobile number
Enter the OTP sent to your number
Change