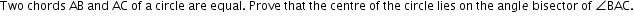CBSE Class 9 Answered
Two circles of radii 10 cm and 17 cm
intersect at two points and distance between their centers is 21 cm. Find the
length of the common chord.
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM

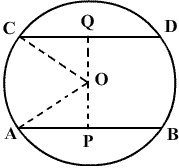
OP
= OQ and ![]() BOQ = 90o
BOQ = 90o
Let OB = x cm, OA = 21 - x cm
In
rt. ![]() AOP,
AOP,
OA2 + OP2 = AP2
(21 - x)2 + OP2 = 172
OP2 = 289 - (21 - x)2
In
rt. ![]() BOP,
BOP,
OB2 + OP2 = BP2
x2 + OP2 = 102
OP2 = 100 - x2
![]() 289 - (21 - x)2 = 100 - x2
289 - (21 - x)2 = 100 - x2
![]() 289 - (441 + x2 - 42x) = 100 - x2
289 - (441 + x2 - 42x) = 100 - x2
![]() 289 - 441 - x2 + 42x = 100 - x2
289 - 441 - x2 + 42x = 100 - x2
![]() 42x = 252
42x = 252
![]() x = 6
x = 6
![]() OP2 = 100 - 62 = 64
OP2 = 100 - 62 = 64
OP = 8
PQ
= 2 ![]() OP = 2
OP = 2 ![]() 8 = 16 cm
8 = 16 cm
Answered by | 04 Jun, 2014, 03:23: PM
Application Videos
Concept Videos
CBSE 9 - Maths
Asked by subbusuchi1978 | 05 Nov, 2023, 10:24: AM
CBSE 9 - Maths
Asked by rameshsonkar1234ramesh | 21 Dec, 2022, 11:03: PM
CBSE 9 - Maths
Asked by chalkekalyani80 | 06 Mar, 2022, 11:25: AM
CBSE 9 - Maths
Asked by tejvinder3r | 27 Jan, 2020, 10:27: AM
CBSE 9 - Maths
Asked by arvindhsb2005 | 14 Jan, 2020, 09:14: PM
CBSE 9 - Maths
Asked by sambitgenius2005 | 24 Apr, 2019, 08:03: PM
CBSE 9 - Maths
Asked by Topperlearning User | 18 Aug, 2017, 09:07: AM
CBSE 9 - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 9 - Maths
Asked by Topperlearning User | 14 Feb, 2014, 02:05: PM