CBSE Class 9: Perpendicular From Centre to Chord Videos | Perpendicular From Centre to Chord
Perpendicular From Centre to Chord
Perpendicular from centre of a circle bisects the chord.
Line segment joining the centre of a circle to the midpoint of a chord is perpendicular to the chord.
The perpendicular bisectors of two chords of a circle intersect at its centre.
There is one and only one circle which passes through 3 non-collinear points.
Line segment joining the centre of a circle to the midpoint of a chord is perpendicular to the chord.
The perpendicular bisectors of two chords of a circle intersect at its centre.
There is one and only one circle which passes through 3 non-collinear points.
More videos from this chapter
View All-
Concepts on angle subtended by a chord at a point ...
-
Properties of Equal Chords
-
Relation between angle subtended by an arc at centre ...
-
Angle subtended by a chord at a point
-
Properties ...
- prove that of all chords of circle through a given point within it, the chord which is bisected at that point is the smallest
- if two circles intersect at two points prove that their centres lie in the perpendicular bisector of the common chord
- three girls Reshma Salma And Mandeep are playing a game by standing on a circle of radius 5 drawn in a park Reshma throws a ball to Salma Salma To mandip mandip to Reshma if the distance between Reshma and Salman and between Salman Mandeep 6 each what is the distance between Reshma Mandip
- two circles of radii 5cm and 3cm intersect at two points and distance between the centres is 4cm. find the length of the common chord
- AC is the diameter of the circle whose centre is O .AB and CD are parallel chords of a circle .prove that OA = OB
- Q. Out of two concentric circles,the radius of the outer circle is 5 cm and the chord AC of length 8 cm is tangent to the inner circle.Find the radius of the inner circle.
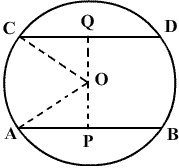
- Prove that the line joining the mid points of two parallel chords of a circle, passes through the centre of the circle.
- Prove that the perpendicular from the centre of the circle to a chord bisects the chord.
-
AB and CD are two parallel chords of a circle such that AB = 12 cm and CD = 24 cm. The chords are on the opposite sides of the centre and the distance between them is 17 cm. Find the distance between them.
-
