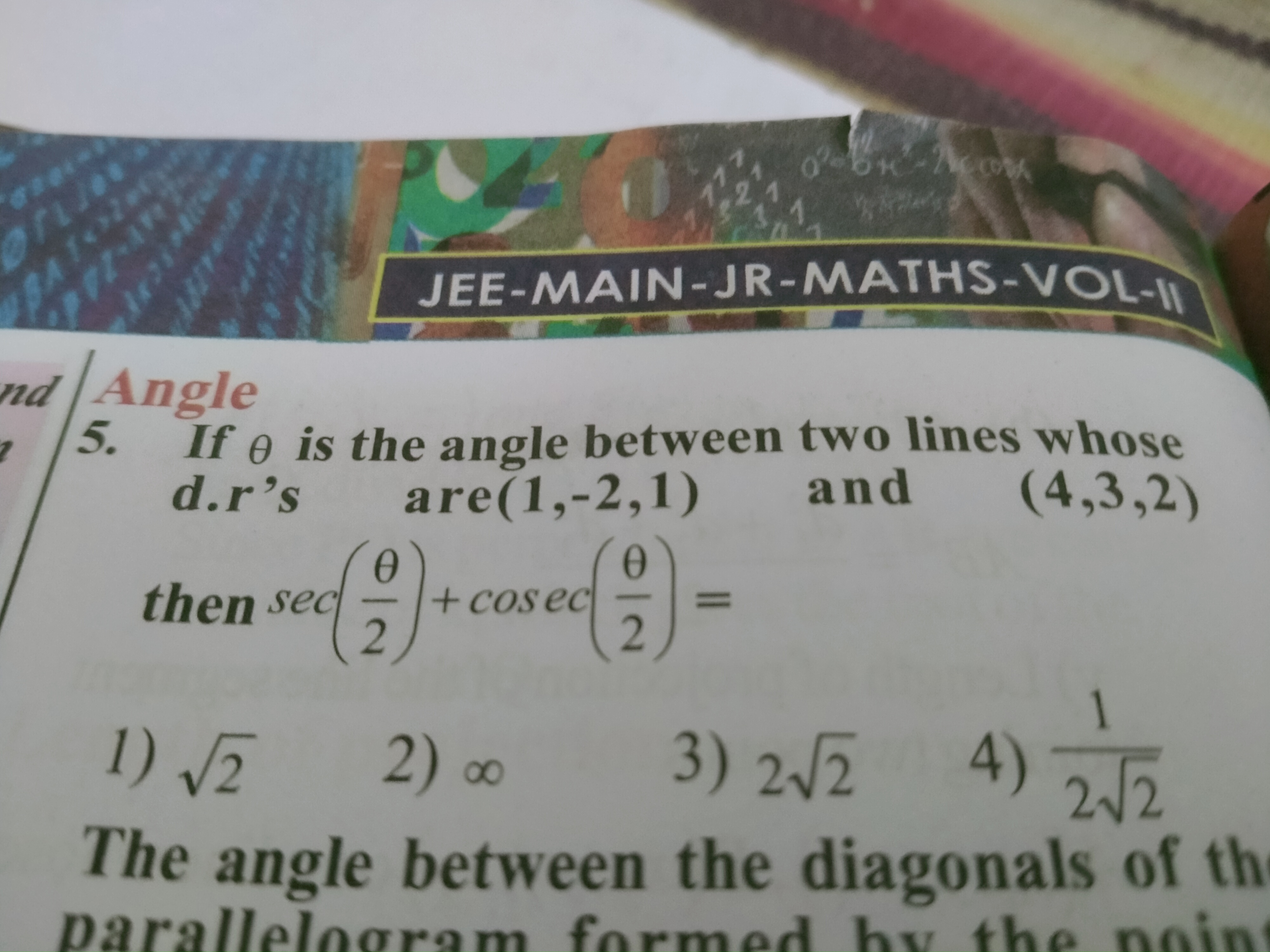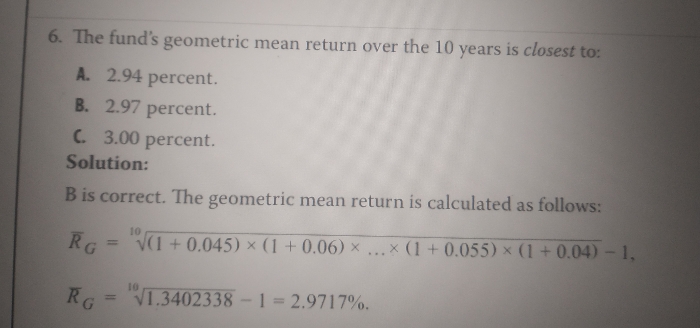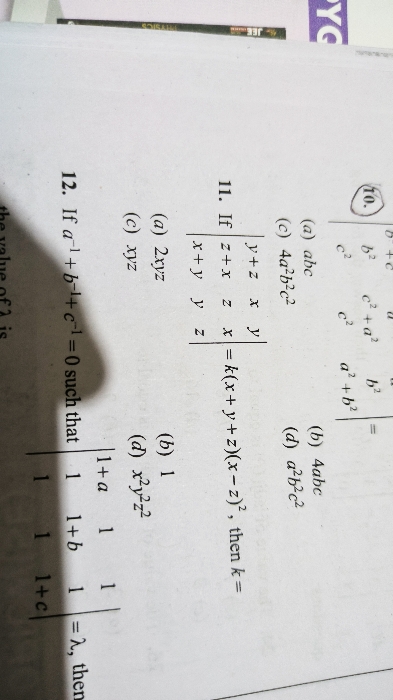JEE Class main Answered
The locus of the centre of a circle which touches two given circles of different radii externally is
Asked by ankitraj875725 | 29 Nov, 2018, 03:54: PM
Expert Answer
Let A and B are the given two circles with radii R1 and R2 respectively and their centres are F and G respectively.
Let C and D are variable circles so that each circle meet the given circles A and B externally.
Let r1 be the radius of circle C and P be its centre. Let r2 be the radius of circle D and Q be its centre.
PF = R1+r1 , PG = R2+r1 , PF-PG = R1 - R2
QF = R1+r2 , QG = R2+r2 , QF-QG = R1 - R2
Hence locus of centres of touching circles is set of points so that the difference between the distances from two given
fixed points ( here F and G ) to the point in locus is constant.
This locus is hyperbola and the fixed points F and G (Centers of given circles ) are foci of hyperbola
Answered by Thiyagarajan K | 30 Nov, 2018, 10:01: AM
Application Videos
-
Finding ratio of lengths of sides of a triangle when th ...
This explains how to find the angles of a triangle using the relation betwe... -
Distance of a point lying on the square and circle from ...
The question solved in this video uses the standard equation of a circle is... -
Area of triangle formed by tangent & normal to circ ...
The video explains how to find the area of a triangle formed by the tangent... -
Solving the DE using variable separation method
The video explains to find the solution of a differential equation using th... -
Solution of a Linear DE using Integrating factor
Question solved in the video explains to find the solution of linear differ...
Concept Videos
-
Properties of Inverse Trigonometry Part - 1
This video explains the properties of inverse trigonometric applications an... -
Trigonometric identities and problems
Fundamental trigonometric identities and problems based on them. Sign Conve... -
Graphical representation of inverse trigonometric funct ...
Graphical representation of inverse trigonometric functions and principle ... -
Degree measure and Radian measure ...
This video explains the concept of negative & positive angles, conversion o... -
Continuous and Discontinuous function
Understand the meaning of function to be continuous and discontinuous, comb...
JEE main - Maths
Asked by kakumanumanoj282 | 20 Apr, 2024, 06:07: PM
ANSWERED BY EXPERTJEE main - Maths
Asked by nirmalraulji5 | 18 Apr, 2024, 09:03: PM
ANSWERED BY EXPERT
JEE main - Maths
Asked by veerababukoppisettiveerababu3 | 17 Apr, 2024, 05:49: PM
ANSWERED BY EXPERTJEE main - Maths
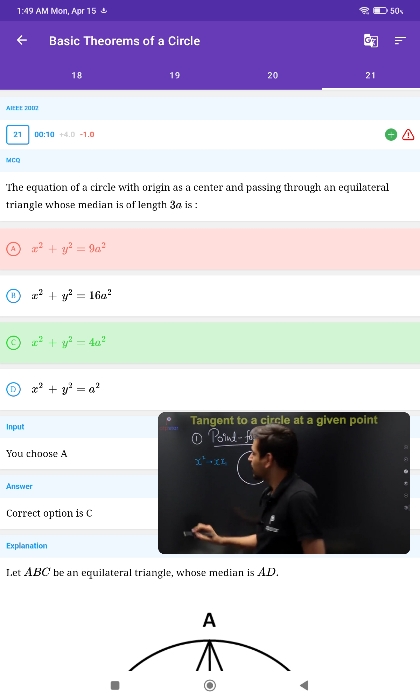
Asked by usakoyalshailesh | 15 Apr, 2024, 09:48: AM
ANSWERED BY EXPERT
JEE main - Maths
Asked by sharmalalita847 | 14 Apr, 2024, 09:21: PM
ANSWERED BY EXPERT
