NEET Class neet Answered

please answer this

Asked by Prashant DIGHE | 06 Dec, 2019, 10:56: PM

Expert Answer

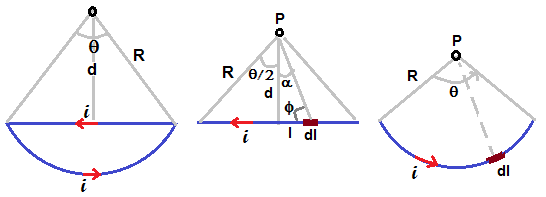
Left side figure shows the current loop made up of circular arc and chord of the same circle. Angle subtended by chord and arc is θ.

To get magnetic induction at P due to current i passing through loop as shown in figure,

let us calculate the magnetic induction separately for arc and chord.

Figure given in the middle helps us to get magentic induction B₁ at P.

Let us consider small current element idl which is at a distance l from the foot of perpendicular drawn from P to chord.

Using Biot-Severt's law, we get, magnetic induction dB due to this current element as

dB = ( μ_o / 4π ) idl sinφ / ( l² + d² ) = ( μ_o / 4π ) idl d / ( l² + d² )^3/2 ...................(1)

let us use the substitution l = d tanα ( see figure )

Hence dl = d sec²α dα

Using these substitutions, eqn.(1) becomes, dB = ( μ_o i / 4π d) cosα dα ................(2)

We get magnetic induction B₁ by integrating eqn.(2) with limits from -θ/2 to +θ/2

B₁ = ( μ_o i / 2π d) sin(θ/2) .....................(3)

since d = R cos(θ/2) , eqn,(3) becomes, B₁ = ( μ_o i / 2π R) tan(θ/2) ...................(4)₁

Direction of this magnetic induction is inward ( please check using right hand rule )

----------------------------------

Right side figure helps us to get magnetic induction at P due to circular arc.

Let us consider current element idl in the circular arc. Magnetic induction dB at P is given by

dB = ( μ_o / 4π ) ( idl / R² )

Magnetic induction B₂ due to full arc will be sum of above dB over arc length Rθ

Hence magnetic induction B₂ = ( μ_o i / 2πR ) ( θ/2 )

Direction of this magnetic induction is outward

--------------------------------------------------------------

net magnetic induction due to loop = B₁ - B₂ = ( μ_o i / 2π R) [ tan(θ/2) - ( θ/2 ) ]

when θ < π , [ tan(θ/2) - ( θ/2 ) ] > 0 , hence direction of net magnetic induction due to loop is inward

when θ > π , [ tan(θ/2) - ( θ/2 ) ] < 0 , hence direction of net magnetic induction due to loop is outwar

---------------------------

Answer to the question :- option (3) inward as long as θ < π

Answered by Thiyagarajan K | 08 Dec, 2019, 08:49: PM

Application Videos