NEET Class neet Answered
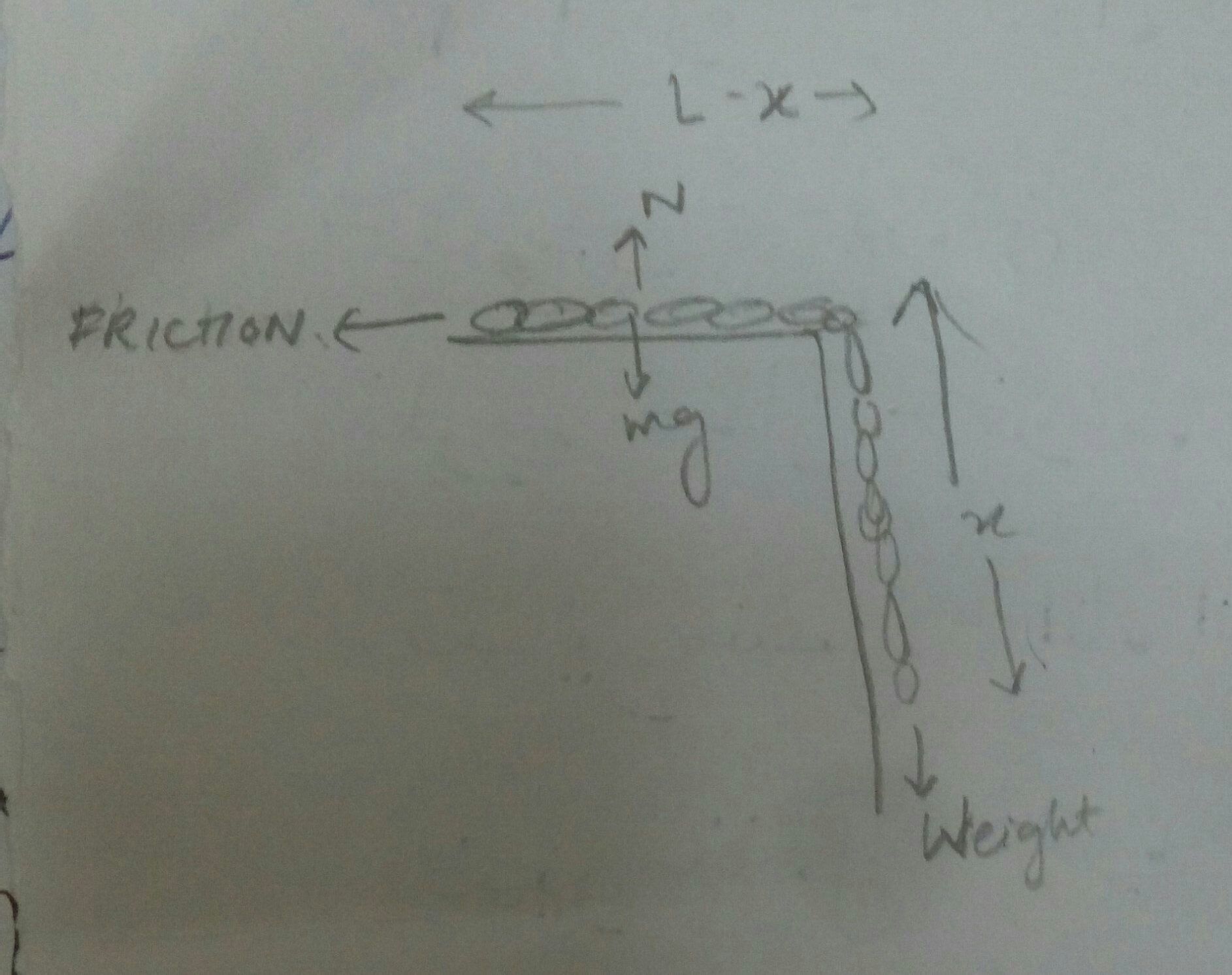
In the chain question in Laws of motion chapter, in which the maximum length of the chain that can hang freely from the table is asked, how is the weight of the chain hanging, whose direction is vertically downwards, said to be balanced by the force of friction in the part of chain lying on the table, whose direction is to the left ? How can forces that are not opposite to each other, byt instead perpendivular to each other, said to balance each other?
Asked by sumayiah2000 | 15 Nov, 2019, 08:05: AM
Expert Answer
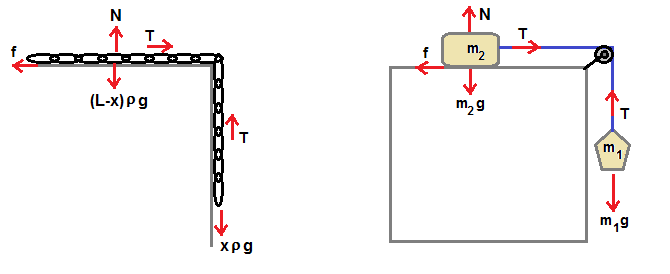
Part of chain hanging on the edge of table as shown in left side figure is similar to
two mass blocks connected by string passing through pulley as shown in right side figure.
In right side figure, block of mass m1 is hanging vertically and pulling the block of mass m2 by
connected string that is passing through pulley.
For the case shown in right side figure, at equilibrium, Tension T in the string balanced by weight m1g .
Since both blocks are connected by same string, same tension T pulling the mass block.
Hence at equilibrium, frciction force is balanced by Tension which is same as the weight of the hanging block m1g.
In same way, for the case of part of chain hanging down at the edge of table,
weight of the hanging part ( x ρ g ) is balanced by the tension T acting on the chain .
Where x is part of the length of the chain hanging, ρ is uniform linear mass density
( ρ = M/L , M is total mass of chain, L is total length of chain ) and g is acceleration due to gravity.
Hence same Tension pulling the part of the chain resting on the table .
Weight of part of the chain resting on the table is [ (L-x) ρ g ] .
Hence normal reaction force provided by table surface N = [ (L-x) ρ g ] .
Hence the friction force f = μ[ (L-x) ρ g ] is balanced by Tension force T = ( x ρ g ) ,
where μ is the friction coefficient
μ[ (L-x) ρ g ] = ( x ρ g ) or x = [ μ / (1+μ) ] L
Answered by Thiyagarajan K | 15 Nov, 2019, 09:28: AM
Application Videos
-
Growth of Current in L-R Circuit
In this video, the growth of current in RL circuit is explained. It include...
NEET neet - Physics
Asked by praveenpriya000079 | 18 Apr, 2024, 07:24: AM
ANSWERED BY EXPERTNEET neet - Physics
Asked by gouranshi84 | 17 Apr, 2024, 05:23: PM
ANSWERED BY EXPERTNEET neet - Physics
Asked by sojusvi | 17 Apr, 2024, 01:12: PM
ANSWERED BY EXPERT
