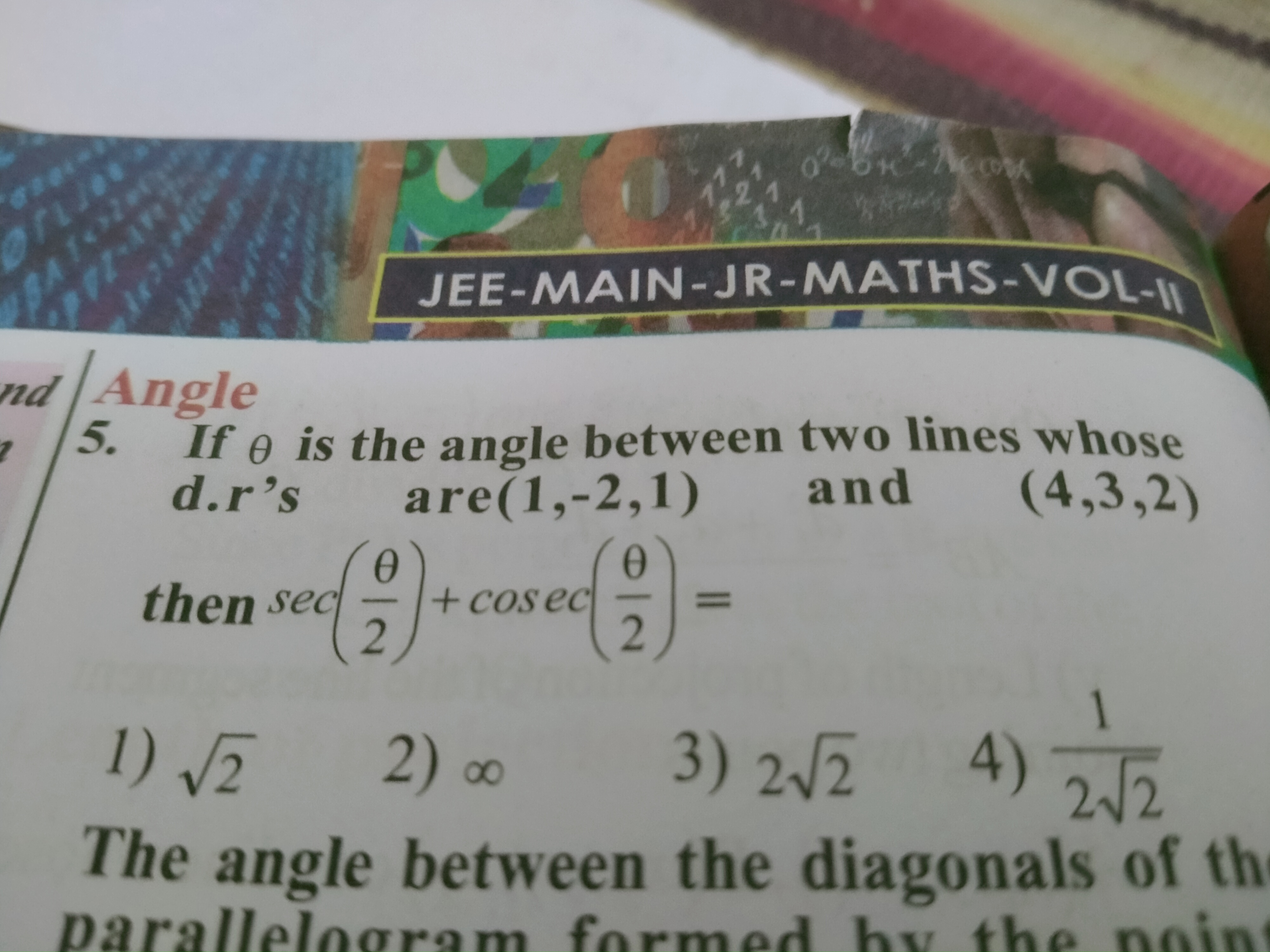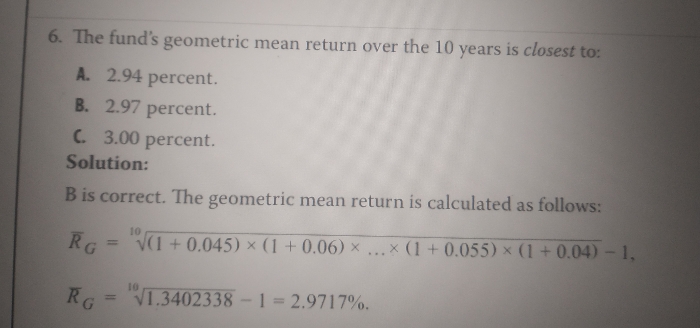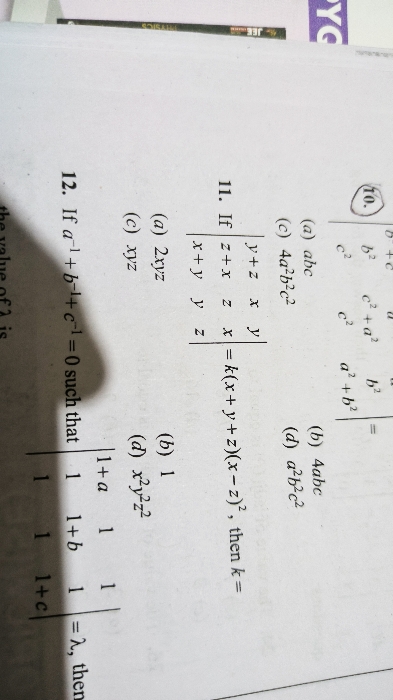Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

JEE Class main Answered

If A ,G, H  be he arithematic geometric and harmonic mean of two numbers a and b then quadratic equation whose roots are A And H May be
Asked by harshitj291 | 10 Mar, 2019, 11:33: AM
answered-by-expert Expert Answer
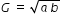
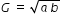
A = (a+b)/2   ;  H = 2ab/(a+b)  ;  begin mathsize 12px style G space equals space square root of a space b end root end style
if roots are A and H,  then the quadtratic equation is , x2 - (A+H)x + (A×H) = 0
 
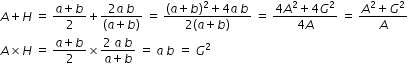
begin mathsize 12px style A plus H space equals space fraction numerator a plus b over denominator 2 end fraction plus fraction numerator 2 a space b over denominator open parentheses a plus b close parentheses end fraction space equals space fraction numerator open parentheses a plus b close parentheses squared plus 4 a space b over denominator 2 open parentheses a plus b close parentheses end fraction space equals space fraction numerator 4 A squared plus 4 G squared over denominator 4 A end fraction space equals space fraction numerator A squared plus G squared over denominator A end fraction A cross times H space equals space fraction numerator a plus b over denominator 2 end fraction cross times fraction numerator 2 space a space b over denominator a plus b end fraction space equals space a space b space equals space G squared end style
 
Hence the quadratic eqn.  is  [  A x2 - ( A2 + G2 ) x + (A G2 ) ] = 0
Answered by Thiyagarajan K | 10 Mar, 2019, 03:25: PM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
JEE main - Maths
solution please
question image
Asked by piyurawriya | 24 Apr, 2024, 12:46: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Maths
answer
question image
Asked by piyurawriya | 23 Apr, 2024, 02:02: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Maths
let M be the skew symmetric orthogonal real matrix.Then only possible eigen values are
Asked by kakumanumanoj282 | 20 Apr, 2024, 06:07: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Maths
sin-1(sin5π/3)
Asked by nirmalraulji5 | 18 Apr, 2024, 09:03: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Maths
1
question image
Asked by hadiabbas803 | 17 Apr, 2024, 07:36: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Maths
Cos66+sin84
Asked by veerababukoppisettiveerababu3 | 17 Apr, 2024, 05:49: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Maths
how to solve this in financial calculator by log
question image
Asked by usakoyalshailesh | 15 Apr, 2024, 09:48: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Maths
dout
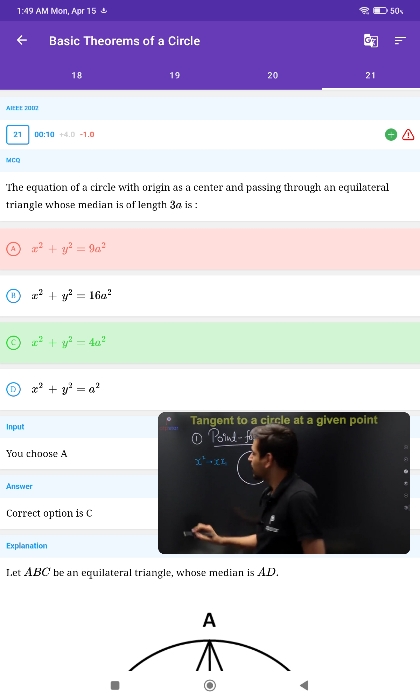
question image
Asked by satnamk123 | 15 Apr, 2024, 01:50: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Maths
I am not able to get the idea for solving this question I know properties of det.
question image
Asked by sharmalalita847 | 14 Apr, 2024, 09:21: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Maths
A∆B=AUB/A'UB'
Asked by sarthakshukla7275 | 14 Apr, 2024, 01:29: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×