CBSE Class 12-science Answered
Dear student,
First of all we find the determinant of given matrix
|
7 |
6 |
x |
|
2 |
x |
2 |
|
x |
3 |
7 |
Expanding by first row, we get the determinant as:
7(7x - 3×2) – 6(2×7 – 2x) + x(2×3 + x×x)
= 7(7x - 6) – 6(14 – 2x) + x(6 – x2)
= 49x – 42 – 84 + 12x + 6x – x3
Rearranging the terms we get
– x3 + (49 + 12 + 6)x – 42 – 84
= – x3 + 67x – 126
Now, this determinant is given to be zero
So,
–x3 + 67x – 126 = 0
Multiplying both sides of above equation by –1, we get
x3 – 67x + 126 = 0 ………………………..(i)
This equation is a cubic, so it must have three roots.
Now, it is also given that one root of the given determinant is x = –9. So, by factor theorem
(x + 9) must be a factor of the polynomial on left hand side of equation (i).
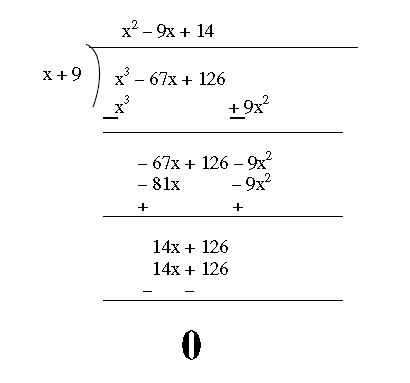
Let us divide x3 – 67x + 126 with (x + 9) to find the other two factors
Divisor = x + 9 and Dividend = x3 – 67x + 126
= (x + 9)(x2 – 7x – 2x + 14)
= (x + 9)[x(x – 7) – 2(x – 7)]
x3 – 67x + 126 = (x + 9)(x – 7)(x – 2) ……………..(ii)
Substituting this value in (i), we get
(x + 9)(x – 7)(x – 2) = 0
So the other two roots are given by x – 7 = 0 and x – 2 = 0 i.e. x = 7 and x = 2

Regards,
Team
TopperLearning
Concept Videos